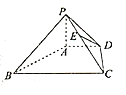
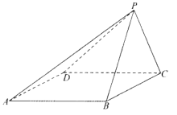
题目内容
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(Ⅰ) 判断函数![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ) 设函数![]() 的定义域为
的定义域为![]() ,且有极值点.
,且有极值点.
(ⅰ) 试判断当![]() 时,
时, ![]() 是否满足题目的条件,并说明理由;
是否满足题目的条件,并说明理由;
(ⅱ) 设函数![]() 的极小值点为
的极小值点为![]() ,求证:
,求证: ![]() .
.
【答案】(Ⅰ)见解析; (Ⅱ) (ⅰ)满足 ,理由见解析 (ⅱ)见解析.
【解析】
(Ⅰ)求![]() ,根据导数与函数单调性的关系,结合参数b的取值范围,分类讨论函数
,根据导数与函数单调性的关系,结合参数b的取值范围,分类讨论函数![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ) (ⅰ)代入b=2,求得![]() ,可判断定义域满足题目的条件,再利用零点存在性定理,判断函数有极点;
,可判断定义域满足题目的条件,再利用零点存在性定理,判断函数有极点;
(ⅱ)先根据满足题目条件,求出b的取值范围,以及b关于x的函数式,并判断![]() 有两个极值点,再根据取极小值时函数式构造函数,利用导数和x0的取值范围,证明不等式成立.
有两个极值点,再根据取极小值时函数式构造函数,利用导数和x0的取值范围,证明不等式成立.
(Ⅰ)![]() ,
,
若![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上递增;
上递增;
若![]() ,由
,由![]() 解得
解得![]() ,
,![]() ,
,
当![]() ,解得
,解得![]() ,此时当
,此时当![]() ,
,![]() ,
,![]() 时,
时,![]() ,结合
,结合![]() 时,x=
时,x=![]()
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
当![]() 时,解得
时,解得![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得-2<
得-2<![]() 或
或![]() ,结合
,结合![]() 时,x=
时,x=![]() 所以
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
综上所述,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减,在
单调递减,在![]() 上单调递增;其中
上单调递增;其中![]() ,
,![]()
(Ⅱ)![]() .
.
(ⅰ)当![]() 时,
时,![]() ,此时
,此时![]() 的定义域为
的定义域为![]() ,
,
![]() ,又
,又![]() ,
,![]()
所以![]() 在
在![]() 上有变号,有零点,
上有变号,有零点,
所以![]() 有极值,即
有极值,即![]() 时,
时,![]() 满足题目的条件.
满足题目的条件.
(ⅱ)![]() ,因为
,因为![]() 的定义域为
的定义域为![]() ,故
,故![]() ,即
,即![]() .
.
![]() ,令
,令![]() ,得
,得![]() ,设
,设![]() ,
,
则![]() ,当
,当![]() 时,
时,![]() ,
,![]() 递增,当
递增,当![]() 时,
时,![]() ,
,![]() 递减,
递减,
所以![]() ,所以
,所以![]() ,即
,即![]() 时,满足
时,满足![]() 的定义域为R且有极点.此时
的定义域为R且有极点.此时![]() 有且只有两个变号零点,一个为
有且只有两个变号零点,一个为![]() 的极大值点,一个为极小值点,且极小值点大于
的极大值点,一个为极小值点,且极小值点大于![]() ,
,
故![]() 且唯一,又
且唯一,又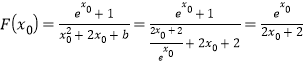 ,
,
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上递增,
上递增,
又4>![]() ,所以
,所以![]() ,结合函数单调性,可判断0<
,结合函数单调性,可判断0<![]() ,
,
所以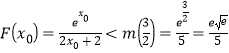 .
.

【题目】为推进“千村百镇计划”,2019年4月某新能源公司开展“电动绿色出行”活动,首批投放200台![]() 型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对
型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对![]() 型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
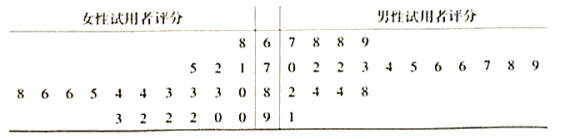
(1)求40个样本数据的中位数![]() ;
;
(2)已知40个样本数据的平均数![]() ,记
,记![]() 与
与![]() 的最大值为
的最大值为![]() .该公司规定样本中试用者的“认定类型”:评分不小于
.该公司规定样本中试用者的“认定类型”:评分不小于![]() 的为“满意型”,评分小于
的为“满意型”,评分小于![]() 的为“需改进型”.
的为“需改进型”.
①请以40个样本数据的频率分布来估计收回的600份评分表中,评分小于![]() 的份数;
的份数;
②请根据40个样本数据,完成下面2×2列联表:
认定类型 性别 | 满意型 | 需改进型 | 合计 |
女性 | 20 | ||
男性 | 20 | ||
合计 | 40 |
根据2×2列联表判断能否有99%的把握认为“认定类型”与性别有关?
附: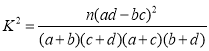 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |