题目内容
3. 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上部同于A、B的一点,且AB=2,PA=BC=1
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上部同于A、B的一点,且AB=2,PA=BC=1(1)求证:平面PAC⊥平面PBC;
(2)求二面角P-BC-A的大小.
分析 (1)根据PA⊥平面ABC便可得到BC⊥PA,又可说明BC⊥AC,从而得到BC⊥平面PAC,从而得出平面PAC⊥平面PBC;
(2)由(1)便知∠PCA为二面角P-BC-A的平面角,根据已知的边的长度,即可求得AC,PA是已知的,从而可求tan∠PCA,从而求出∠PCA.
解答 解:(1)证明:PA⊥平面ABC,BC?平面ABC;
∴PA⊥BC,即BC⊥AC;
又C是⊙O上异于A,B的一点,AB为直径;
∴BC⊥AC,AC∩PA=A;
∴BC⊥平面PAC,BC?平面PBC;
∴平面PAC⊥平面PBC;
(2)BC⊥平面PAC,PC?平面PAC;
∴BC⊥PC,又BC⊥AC;
∴∠PCA是二面角P-BC-A的平面角;
在Rt△ABC中,AB=2,BC=1,∴AC=$\sqrt{3}$;
在Rt△PAC中,$PA=1,AC=\sqrt{3}$,∴$tan∠PCA=\frac{\sqrt{3}}{3}$;
∴∠PCA=30°;
即二面角P-BC-A的大小为30°.
点评 考查线面垂直的性质,线面垂直的判定定理,面面垂直的判定定理,以及直径所对圆周角为直角,直角三角形边的关系,二面角的平面角的概念及求法.

练习册系列答案
相关题目
8.已知Rt△ABC中,AB=AC=a,AD是斜边上的高,以AD为折痕使∠BDC成直角.则折后几何体中,∠BAC的度数为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
 如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BAD=60°.
如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BAD=60°.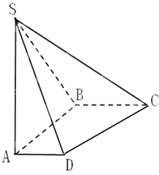 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$ 如图,正四棱锥P-ABCD的顶点都在同一球面上,已知ABCD中心为E,球心O在线段PE上,QA⊥底面ABCD,且与球面交于点Q,若球的半径为2.
如图,正四棱锥P-ABCD的顶点都在同一球面上,已知ABCD中心为E,球心O在线段PE上,QA⊥底面ABCD,且与球面交于点Q,若球的半径为2. 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE. 四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列
四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列