题目内容
 如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D,PD=PC=AD=
如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D,PD=PC=AD=| 2 |
(1)求证:PD⊥平面PBC;
(2)若AA1=a,求a值;
(3)求点C1到平面PAB的距离;
(4)若点P,A,D,C1在同一球面上,求此球面的面积.
分析:(1)要证线面垂直,只需证线线垂直.据PD=PC=
,AB=2,可得PD⊥PC;BC⊥平面PDC,可得PD⊥BC,从而得证.
(2)若PC∥平面AB1D,据线面平行的性质定理可得PC∥DC1,知∠CDC1=∠PCD=45°,则AA1=CD=2即可.
(3)欲求点C到平面PAB的距离,直接由点C作平面PAB的垂线,需补形,不易作出,考虑用等积法完成,十分简洁.
(4)在条件及(2)的前提下,可知PD,PA,PC1两两垂直,引导学生分析:点P,A,D,C1所在的球面就是以PD,DC1,AD为相邻三条棱的长方体的外接球面,从而可求此球面的直径,可求出球面的面积.
| 2 |
(2)若PC∥平面AB1D,据线面平行的性质定理可得PC∥DC1,知∠CDC1=∠PCD=45°,则AA1=CD=2即可.
(3)欲求点C到平面PAB的距离,直接由点C作平面PAB的垂线,需补形,不易作出,考虑用等积法完成,十分简洁.
(4)在条件及(2)的前提下,可知PD,PA,PC1两两垂直,引导学生分析:点P,A,D,C1所在的球面就是以PD,DC1,AD为相邻三条棱的长方体的外接球面,从而可求此球面的直径,可求出球面的面积.
解答:证明:(1)∵ABCD-A1B1C1D1是一个长方体,
∴BC⊥平面CC1D1D,
∵P∈平面CC1D1D,
∴PD?平面CC1D1D,
∴PD⊥BC.
∵PD=PC=
,AB=2,
∴△PCD为等腰直角三角形,
∴PD⊥PC.
∵PD垂直于平面PBC内的两条相交直线PC和BC,
∴PD⊥平面PBC.
解:(2)当a=2时,四边形CC1D1D是一个正方形,
∴∠CDC1=45°,
∵∠PCD=45°,
又PC和C1D在同一个平面内,
∴PC∥DC1,
∵DC1?平面AB1D,PC?平面AB1D,
∴PC∥平面AB1D.
(3)过点P作PE⊥CD交CD于E,
∵面ABCD⊥面PDC,面ABCD∩面PDC=CD,
∴PE⊥平面ABCD,
∴PE=1.
连接AC,设点C到平面PAB的距离为h,
三棱锥P-ABC的体积与三棱锥C-PAB的体积相等,
则
S△ABC•PE=
S△PAB•h,
∵PA=PD=2,AB=2,
∴S△PAB=
×2×
×2=
,
S△ABC=
×2×
=
,
∴
×
×1=
×
h,h=
,
∴点C到平面PAB的距离为
.
(4)∵AD⊥平面CC1D1D(6),PD,DC1在平面CC1D1D内,
AD⊥PD,AD⊥DC1,
由(2)知∠PDC1=90°,
即PD⊥DC1,
∴PD,PA,PC1两两垂直,
∴点P,A,D,C1所在的球面就是以PD,DC1,AD为相邻三条棱的长方体的外接球面,
∵PD=AD=
,DC1=2
,
∴此球面的直径2R=2
,
∴球面的半径R=
,
∴所求球面的面积为4πR2=4π(
)2=12π.
∴BC⊥平面CC1D1D,
∵P∈平面CC1D1D,
∴PD?平面CC1D1D,
∴PD⊥BC.
∵PD=PC=
| 2 |
∴△PCD为等腰直角三角形,
∴PD⊥PC.
∵PD垂直于平面PBC内的两条相交直线PC和BC,
∴PD⊥平面PBC.
解:(2)当a=2时,四边形CC1D1D是一个正方形,
∴∠CDC1=45°,
∵∠PCD=45°,
又PC和C1D在同一个平面内,
∴PC∥DC1,
∵DC1?平面AB1D,PC?平面AB1D,
∴PC∥平面AB1D.
(3)过点P作PE⊥CD交CD于E,
∵面ABCD⊥面PDC,面ABCD∩面PDC=CD,
∴PE⊥平面ABCD,
∴PE=1.
连接AC,设点C到平面PAB的距离为h,
三棱锥P-ABC的体积与三棱锥C-PAB的体积相等,
则
| 1 |
| 3 |
| 1 |
| 3 |
∵PA=PD=2,AB=2,
∴S△PAB=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
S△ABC=
| 1 |
| 2 |
| 2 |
| 2 |
∴
| 1 |
| 3 |
| 2 |
| 1 |
| 3 |
| 3 |
| ||
| 3 |
∴点C到平面PAB的距离为
| ||
| 3 |
(4)∵AD⊥平面CC1D1D(6),PD,DC1在平面CC1D1D内,
AD⊥PD,AD⊥DC1,
由(2)知∠PDC1=90°,
即PD⊥DC1,
∴PD,PA,PC1两两垂直,
∴点P,A,D,C1所在的球面就是以PD,DC1,AD为相邻三条棱的长方体的外接球面,
∵PD=AD=
| 2 |
| 2 |
∴此球面的直径2R=2
| 3 |
∴球面的半径R=
| 3 |
∴所求球面的面积为4πR2=4π(
| 3 |
点评:本题考查点、线、面间的距离和计算,综合性性,难度大,是高考的重点,计算繁琐,容易出错.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.解题时要认真审题,注意化立体问题为平面问题.

练习册系列答案
相关题目
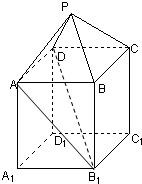 如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且
如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且
 (2008•佛山一模)如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且
(2008•佛山一模)如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且 如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D,
如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D,