题目内容
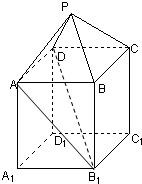 如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且PD=PC=
如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且PD=PC=| 2 |
(Ⅰ)证明:PD⊥平面PBC;
(Ⅱ)若AA1=a,当a为何值时,PC∥平面AB1D.
分析:对于(Ⅰ),要证明PD⊥平面PBC,只需证明PD垂直于平面PBC的两条相交直线即可,由PD=PC=
可得PD⊥PC,而ABCD-A1B1C1D1是一个长方体,容易证明BC⊥面CC1D1D,而P∈平面CC1D1D,所以PD?面CC1D1D,容易得到PD⊥BC,从而得证;
对于(Ⅱ),由于AB1∥DC1,要证PC∥平面AB1D,只需证明PC∥DC1,如右图,只需证明∠PCC1与∠DC1C互补即可,由于∠PCC1=1350,所以∠DC1C=45°,即AA1=a=2.
| 2 |
对于(Ⅱ),由于AB1∥DC1,要证PC∥平面AB1D,只需证明PC∥DC1,如右图,只需证明∠PCC1与∠DC1C互补即可,由于∠PCC1=1350,所以∠DC1C=45°,即AA1=a=2.
解答:解:(Ⅰ)证明:因为PD=PC=
,CD=AB=2,所以△PCD为等腰直角三角形,所以PD⊥PC.(1分)
因为ABCD-A1B1C1D1是一个长方体,所以BC⊥面CC1D1D,而P∈平面CC1D1D,所以PD?面CC1D1D,所以BC⊥PD.(3分)
因为PD垂直于平面PBC内的两条相交直线PC和BC,由线面垂直的判定定理,可得PD⊥平面PBC.(6分)
(Ⅱ)当a=2时,PC∥平面AB1D.(9分)
当a=2时,四边形CC1D1D是一个正方形,所以∠C1DC=45°,而∠PDC=45°,所以∠PDC1=900,所以C1D⊥PD.(12分)
而PC⊥PD,C1D与PC在同一个平面内,所以PC∥C1D.(13分)
而C1D?面AB1C1D,所以PC∥面AB1C1D,所以PC∥平面AB1D.(14分)
| 2 |
因为ABCD-A1B1C1D1是一个长方体,所以BC⊥面CC1D1D,而P∈平面CC1D1D,所以PD?面CC1D1D,所以BC⊥PD.(3分)
因为PD垂直于平面PBC内的两条相交直线PC和BC,由线面垂直的判定定理,可得PD⊥平面PBC.(6分)
(Ⅱ)当a=2时,PC∥平面AB1D.(9分)
当a=2时,四边形CC1D1D是一个正方形,所以∠C1DC=45°,而∠PDC=45°,所以∠PDC1=900,所以C1D⊥PD.(12分)
而PC⊥PD,C1D与PC在同一个平面内,所以PC∥C1D.(13分)
而C1D?面AB1C1D,所以PC∥面AB1C1D,所以PC∥平面AB1D.(14分)
点评:本题考查线面垂直的判定及线面平行的判定,要注意线面垂直中的转化思想,第二问中要注意转化到平面内进行证明与判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 (2008•佛山一模)如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且
(2008•佛山一模)如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且 如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D,
如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D, 如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D,
如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D,