题目内容
如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AA1=a,AB=2,BC=3,点P∈平面CC1D1D且PD=PC=
.

(Ⅰ)在正视图右边及下方区域画出其侧视图、俯视图(在答卷上作答)
(II)证明:PD⊥平面PBC;
(III)证明:当a=2时,PC∥平面AB1D.
| 2 |

(Ⅰ)在正视图右边及下方区域画出其侧视图、俯视图(在答卷上作答)
(II)证明:PD⊥平面PBC;
(III)证明:当a=2时,PC∥平面AB1D.
分析:(I)利用长对正,宽相等,高平齐,即可得到侧视图、俯视图;
(II)证明PD⊥PC,PD⊥PC,利用线面垂直的判定定理,即可得到结论;
(III)证明PC∥C1D,利用线面平行的判定定理,可得结论.
(II)证明PD⊥PC,PD⊥PC,利用线面垂直的判定定理,即可得到结论;
(III)证明PC∥C1D,利用线面平行的判定定理,可得结论.
解答: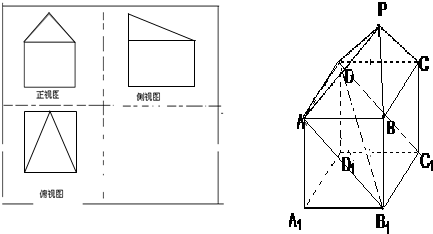 (I)解:如图所示;
(I)解:如图所示;
(II)证明:
因为PD=PC=
,
CD=AB=2,
所以△PCD为等腰直角三角形,所以PD⊥PC.(5分)
因为ABCD-A1B1C1D1是一个长方体,
所以BC⊥面CC1D1D,(6分)
而P∈平面CC1D1D,所以PD?面CC1D1D,所以PD⊥PC. …(7分)
又PC和BC为平面PBC内的两条相交直线,(8分)
所以PD⊥平面PBC. …(9分)
(III)解:长方体中AD∥BC,AD=BC,BC∥B1C1,BC=B1C1,
∴AD∥B1C1,AD=B1C1
∴A,D,B1,C1共面 …(10分)
长方体中DD1=AA1=a=2,CD=AB=2,四边形CC1D1D是一个正方形,∠C1DC=45°,
而∠PCD=45°,且CD、C1D与PC在同一个平面内,…(11分)
所以PC∥C1D. …(12分)
又C1D?面AB1C1D,PC?面AB1C1D…(13分)
所以PC∥面AB1C1D,即PC∥平面AB1D. …(14分)
 (I)解:如图所示;
(I)解:如图所示;(II)证明:
因为PD=PC=
| 2 |
CD=AB=2,
所以△PCD为等腰直角三角形,所以PD⊥PC.(5分)
因为ABCD-A1B1C1D1是一个长方体,
所以BC⊥面CC1D1D,(6分)
而P∈平面CC1D1D,所以PD?面CC1D1D,所以PD⊥PC. …(7分)
又PC和BC为平面PBC内的两条相交直线,(8分)
所以PD⊥平面PBC. …(9分)
(III)解:长方体中AD∥BC,AD=BC,BC∥B1C1,BC=B1C1,
∴AD∥B1C1,AD=B1C1
∴A,D,B1,C1共面 …(10分)
长方体中DD1=AA1=a=2,CD=AB=2,四边形CC1D1D是一个正方形,∠C1DC=45°,
而∠PCD=45°,且CD、C1D与PC在同一个平面内,…(11分)
所以PC∥C1D. …(12分)
又C1D?面AB1C1D,PC?面AB1C1D…(13分)
所以PC∥面AB1C1D,即PC∥平面AB1D. …(14分)
点评:本题考查线面垂直,考查线面平行,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
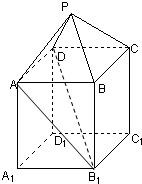 如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且
如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且 (2008•佛山一模)如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且
(2008•佛山一模)如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且 如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D,
如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D, 如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D,
如图.在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,且AB=2,P∈平面CC1D1D,