题目内容
已知直线 经过直线3x+4y-2=0与直线2x+y+2=0的交点P,且垂直于直线x-2y-1=0。
经过直线3x+4y-2=0与直线2x+y+2=0的交点P,且垂直于直线x-2y-1=0。
(Ⅰ)求直线 的方程;
的方程;
(Ⅱ)求直线 与两坐标轴围成的三角形的面积S。
与两坐标轴围成的三角形的面积S。
 经过直线3x+4y-2=0与直线2x+y+2=0的交点P,且垂直于直线x-2y-1=0。
经过直线3x+4y-2=0与直线2x+y+2=0的交点P,且垂直于直线x-2y-1=0。(Ⅰ)求直线
 的方程;
的方程;(Ⅱ)求直线
 与两坐标轴围成的三角形的面积S。
与两坐标轴围成的三角形的面积S。 解:(Ⅰ)由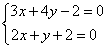 ,解得:
,解得: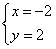 ,
,
所以点P的坐标是(-2,2),则所求直线 与x-2y-1=0垂直,
与x-2y-1=0垂直,
可设直线 的方程为2x+y+c=0,
的方程为2x+y+c=0,
把点P的坐标代入,得2×(-2)+2+c=0,即c=2,
所以,所求直线的方程为2x+y+2=0。
(Ⅱ)由直线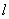 的方程知它在x轴、y轴上的截距分别是-1、-2,
的方程知它在x轴、y轴上的截距分别是-1、-2,
所以直线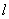 与两坐标轴围成三角形的面积
与两坐标轴围成三角形的面积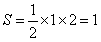 。
。
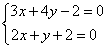 ,解得:
,解得: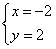 ,
,所以点P的坐标是(-2,2),则所求直线
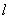 与x-2y-1=0垂直,
与x-2y-1=0垂直,可设直线
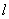 的方程为2x+y+c=0,
的方程为2x+y+c=0,把点P的坐标代入,得2×(-2)+2+c=0,即c=2,
所以,所求直线的方程为2x+y+2=0。
(Ⅱ)由直线
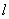 的方程知它在x轴、y轴上的截距分别是-1、-2,
的方程知它在x轴、y轴上的截距分别是-1、-2, 所以直线
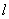 与两坐标轴围成三角形的面积
与两坐标轴围成三角形的面积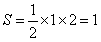 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目