题目内容
已知函数f（x）=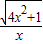
（x＞0）．（1）求数列{an}满足a1=1，
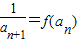，求an；（2）若bn=an+12+an+22+…+a2n+12，是否存在最小正整数P，使对任意x∈N*，都有bn＜
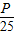成立．
【答案】分析：（1）根据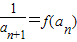
化简可得数列{
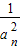}是首项为1，公差为4的等差数列，求出数列{
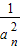}通项，从而求出an；
（2）根据（1）可求出bn，从而求出bn+1，将两式作差得bn+1-bn＜0，得到{bn}是递减数列，存在最大项b1，只需b1＜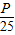
求出P，即可求出所求．
解答：解：（1）由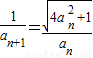
得
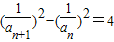
∴数列{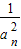
}是首项为1，公差为4的等差数列
∴
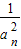=4n-3，又an＞0，所以an=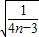
（2）根据（1）得bn=an+12+an+22+…+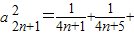
…+
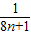
bn+1=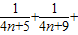
…+
因为bn+1-bn=
，所以{bn}是递减数列
存在最大项b1=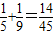
，依题意，只需
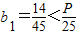，解得P＞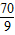
又P∈N*，所以存在最小正整数P=8，使不等式成立．
点评：本题主要考查了等差数列的判定，以及数列的通项公式和数列与函数的综合、数列与不等式的综合，同时考查了计算能力，属于中档题．
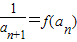化简可得数列{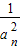}是首项为1，公差为4的等差数列，求出数列{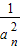}通项，从而求出an；（2）根据（1）可求出bn，从而求出bn+1，将两式作差得bn+1-bn＜0，得到{bn}是递减数列，存在最大项b1，只需b1＜
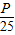求出P，即可求出所求．解答：解：（1）由
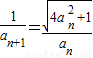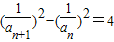
得∴数列{
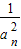}是首项为1，公差为4的等差数列∴
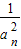=4n-3，又an＞0，所以an=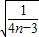（2）根据（1）得bn=an+12+an+22+…+
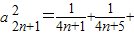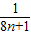
…+bn+1=
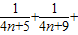…+因为bn+1-bn=
，所以{bn}是递减数列存在最大项b1=
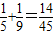，依题意，只需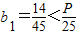，解得P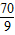＞又P∈N*，所以存在最小正整数P=8，使不等式成立．
点评：本题主要考查了等差数列的判定，以及数列的通项公式和数列与函数的综合、数列与不等式的综合，同时考查了计算能力，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|