题目内容
已知向量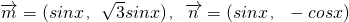 ,设函数
,设函数 .
.
(Ⅰ)求函数f(x)在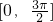 上的单调递增区间;
上的单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,若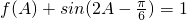 ,b+c=7,△ABC的面积为
,b+c=7,△ABC的面积为 ,求边a的长.
,求边a的长.
解:(Ⅰ)由题意得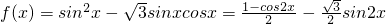 =
=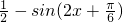 …(3分)
…(3分)
令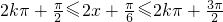 ,k∈Z
,k∈Z
解得: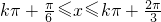 ,k∈Z
,k∈Z
∵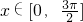 ,∴
,∴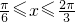 ,或
,或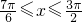
所以函数f(x)在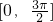 上的单调递增区间为
上的单调递增区间为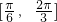 ,
, …(6分)
…(6分)
(Ⅱ)由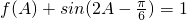 得:
得: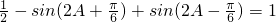
化简得: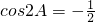
又因为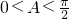 ,解得:
,解得: …(9分)
…(9分)
由题意知: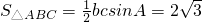 ,解得bc=8,
,解得bc=8,
又b+c=7,所以a2=b2+c2-2bccosA=(b+c)2-2bc(1+cosA)=
故所求边a的长为5.…(12分)
分析:(Ⅰ)利用向量的数量积公式,结合辅助角公式化简函数,再利用正弦函数的单调性,结合函数的定义域,即可得到结论;
(Ⅱ)由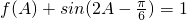 ,可得
,可得 ,利用△ABC的面积为
,利用△ABC的面积为 ,结合余弦定理,即可求边a的长.
,结合余弦定理,即可求边a的长.
点评:本题考查向量知识的运用,考查三角函数的化简与三角函数的性质,考查余弦定理的运用,正确化简函数是关键.
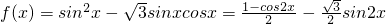 =
=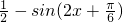 …(3分)
…(3分)令
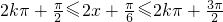 ,k∈Z
,k∈Z解得:
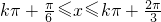 ,k∈Z
,k∈Z∵
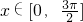 ,∴
,∴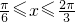 ,或
,或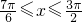
所以函数f(x)在
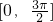 上的单调递增区间为
上的单调递增区间为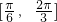 ,
, …(6分)
…(6分)(Ⅱ)由
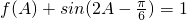 得:
得: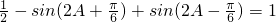
化简得:
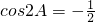
又因为
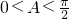 ,解得:
,解得: …(9分)
…(9分)由题意知:
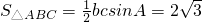 ,解得bc=8,
,解得bc=8,又b+c=7,所以a2=b2+c2-2bccosA=(b+c)2-2bc(1+cosA)=

故所求边a的长为5.…(12分)
分析:(Ⅰ)利用向量的数量积公式,结合辅助角公式化简函数,再利用正弦函数的单调性,结合函数的定义域,即可得到结论;
(Ⅱ)由
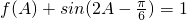 ,可得
,可得 ,利用△ABC的面积为
,利用△ABC的面积为 ,结合余弦定理,即可求边a的长.
,结合余弦定理,即可求边a的长.点评:本题考查向量知识的运用,考查三角函数的化简与三角函数的性质,考查余弦定理的运用,正确化简函数是关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目

 ,设函数
,设函数
 的图象关于直线
的图象关于直线 对称,其中常数
对称,其中常数
 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图像,用五点法作出函数
的图像,用五点法作出函数 的图像.
的图像. ,设函数
,设函数 ;
; 求函数f(x)的最值及对应的x的值;-
求函数f(x)的最值及对应的x的值;- 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. ,设函数
,设函数 .
. ,求f(A+B)的值.
,求f(A+B)的值. ,
, 设函数
设函数 .
. 求
求 的最小正周期与单调递增区间;
的最小正周期与单调递增区间; 在
在 中,
中, 分别是角
分别是角 的对边,若
的对边,若 ,
, ,求
,求 的最大值.
的最大值.