题目内容
在△ABC中,BC=
,AC=3,sinC=2sinA.
(Ⅰ)求AB的值;
(Ⅱ)求sin(2A-
)的值.
| 5 |
(Ⅰ)求AB的值;
(Ⅱ)求sin(2A-
| π |
| 4 |
(Ⅰ)在△ABC中,BC=
,AC=3,sinC=2sinA,
则根据正弦定理
=
得:
AB=sinC
=2BC=2
;
(Ⅱ)在△ABC中,AB=2
,BC=
,AC=3,
∴根据余弦定理得:cosA=
=
,
又A为三角形的内角,则sinA=
=
,
从而sin2A=2sinAcosA=
,cos2A=cos2A-sin2A=
,
则sin(2A-
)=sin2Acos
-cos2Asin
=
.
| 5 |
则根据正弦定理
| AB |
| sinC |
| BC |
| sinA |
AB=sinC
| BC |
| sinA |
| 5 |
(Ⅱ)在△ABC中,AB=2
| 5 |
| 5 |
∴根据余弦定理得:cosA=
| AB2+AC2-BC2 |
| 2AB•AC |
2
| ||
| 5 |
又A为三角形的内角,则sinA=
| 1-cos2A |
| ||
| 5 |
从而sin2A=2sinAcosA=
| 4 |
| 5 |
| 3 |
| 5 |
则sin(2A-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 10 |

练习册系列答案
相关题目
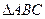 中,
中,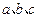 分别为角
分别为角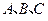 的对边,且满足
的对边,且满足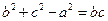 .
.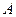 的值;
的值;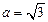 ,设角
,设角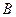 的大小为
的大小为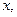
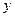 ,求
,求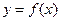 的最大值.
的最大值.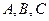 的对边分别为
的对边分别为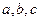 ,且满足
,且满足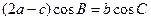 . (Ⅰ)求角B的大小; (Ⅱ)设
. (Ⅰ)求角B的大小; (Ⅱ)设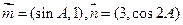 ,试求
,试求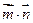 的取值范围.
的取值范围.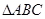 中,角
中,角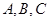 所对的边分别为
所对的边分别为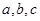 ,若
,若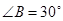 ,
,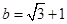 ,则
,则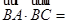 .
. 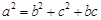 ,则A等于 ( ).
,则A等于 ( ).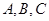 的对边分别为
的对边分别为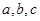 ,若
,若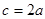 ,则
,则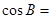 ( )
( ) 
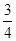
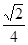
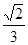
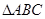 中,若
中,若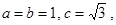 则角
则角