题目内容
某校高一某班的一次数学测试成绩(满分100分)的茎叶图和频率分布直方图都受到不同程度的污染,但可见部分如下,据此解答如下问题:
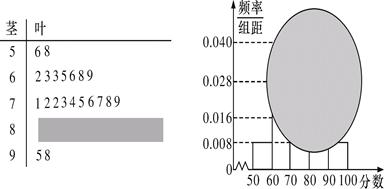
(Ⅰ) 求分数在[50,60)的频率及全班人数;
(Ⅱ) 求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(Ⅲ)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
【答案】
(Ⅰ)分数在[50,60)之间的频数为2,所以全班人数为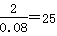 , (Ⅱ) 0.016,(Ⅲ) 0.6
, (Ⅱ) 0.016,(Ⅲ) 0.6
【解析】
试题分析:(Ⅰ) 分数在[50,60)的频率为0.008×10=0.08,
由茎叶图知:分数在[50,60)之间的频数为2,所以全班人数为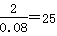 , 3分
, 3分
(Ⅱ) 分数在[80,90)之间的频数为25-2-7-10-2=4;
频率分布直方图中[80,90)间的矩形的高为 .
6分
.
6分
(Ⅲ)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,
在[80,100]之间的试卷中任取两份的基本事件为:
(1,2),(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),
(3,4),(3,5),(3,6),
(4,5),(4,6),
(5,6)共15个,
其中,至少有一个在[90,100]之间的基本事件有9个,
故至少有一份分数在[90,100]之间的概率是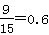 12分
12分
考点:本题考查了频率分布直方图的运用及古典概型的求法
点评:注意频率分布直方图中用小长方形面积的大小来表示在各个区间内取值的频率,所以在求面积时,通过已知求出所要区间的面积即可

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
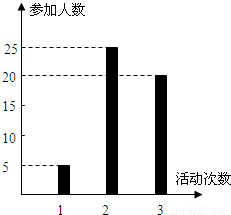
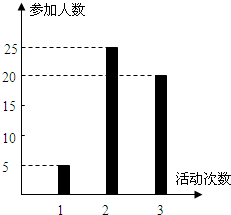 按照新课程的要求,高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).某校高一•一班50名学生在上学期参加活动的次数统计如条形图所示.
按照新课程的要求,高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).某校高一•一班50名学生在上学期参加活动的次数统计如条形图所示.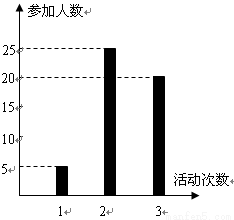
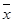 ;
;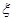 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量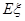 .(要求:答案用最简分数表示)
.(要求:答案用最简分数表示) ;
;