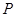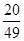Question

（本小题满分12分）

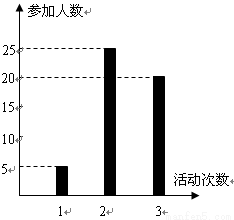
       按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动（以下简称活动）．某校高一·一班50名学生在上学期参加活动的次数统计如条形图所示．

   （Ⅰ）求该班学生参加活动的人均次数；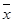

   （Ⅱ）从该班中任意选两名学生，求他们参加活动次数恰好相等的概率；

   （Ⅲ）从该班中任选两名学生，用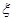表示这两人参加活动次数之差的绝对值，求随机变量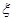的分布列及数学期望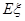．（要求：答案用最简分数表示）

 

Answer 1

【答案】

（Ⅰ）=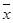

（Ⅱ）

（Ⅲ）见解析

【解析】由图可知，参加活动1次、2次和3次的学生人数分别为5、25和20．

（Ⅰ）该班学生参加活动的人均次数为=．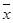

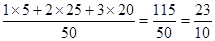（Ⅱ）从该班中任选两名学生，他们参加活动次数恰好相等的概率为

       ．

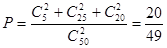（Ⅲ）从该班中任选两名学生，记“这两人中一人参加1次活动，另一人参加2次活动”为事件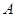，“这两人中一人参加2次活动，另一人参加3次活动”为事件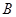，“这两人中一人参加1次活动，另一人参加3次活动”为事件．

       易知；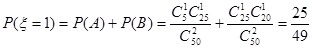

       ．

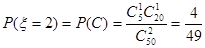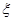       的分布列：

	0	1	2

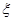       的数学期望：．