题目内容
在△ABC中,3sinA+4cosB=6,4sinB+3cosA=1,则∠C的大小为 .
【答案】分析:由题意两式相加平方求出sinC,判断C是否满足题意即可.
解答:解:两式平方相加可得9+16+24sin(A+B)=37,
sin(A+B)=sinC= ,
,
所以C=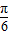 或
或 π.如果C=
π.如果C= π,则0<A<
π,则0<A<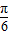 ,从而cosA>
,从而cosA>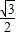 ,3cosA>1
,3cosA>1
与4sinB+3cosA=1矛盾(因为4sinB>0恒成立),
故C=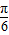 .
.
故答案为: .
.
点评:本题是基础题,考查三角函数的化简求值,注意角的范围的判断,是本题的易错点.
解答:解:两式平方相加可得9+16+24sin(A+B)=37,
sin(A+B)=sinC=
 ,
,所以C=
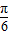 或
或 π.如果C=
π.如果C= π,则0<A<
π,则0<A<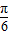 ,从而cosA>
,从而cosA>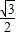 ,3cosA>1
,3cosA>1与4sinB+3cosA=1矛盾(因为4sinB>0恒成立),
故C=
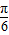 .
.故答案为:
 .
.点评:本题是基础题,考查三角函数的化简求值,注意角的范围的判断,是本题的易错点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,3sinA+4cosB=6,3cosA+4sinB=1,则∠C的大小为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,3sinA+4cosB=6,4sinB+3cosA=1,则C等于( )
| A、30° | B、150° | C、30°或150° | D、60°或120° |