题目内容
给出下列命题:①若{an}成等比数列,Sn是前n项和,则S4,S8-S4,S12-S8成等比数列;②已知函数y=2sin(ωx+θ)为偶函数(0<θ<π),其图象与直线y=2的交点的横坐标为x1、x2,若|x1-x2|的最小值为π,则ω的值为2,θ的值为 ;③正弦函数在第一象限为单调递增函数;④函数y=2sin(2x-
;③正弦函数在第一象限为单调递增函数;④函数y=2sin(2x- )的图象的一个对称点是(
)的图象的一个对称点是( ,0);其中正确命题的序号是 .(把你认为正确命题的序号都填上)
,0);其中正确命题的序号是 .(把你认为正确命题的序号都填上)
【答案】分析:由等比数列的性质,可以判断①的真假,由正弦型函数的性质,可以判断②的真假;由函数单调性的局部性及象限角的定义,可以判断③的真假;由正弦型函数的对称性,可以判断④的真假,进而得到答案.
解答:解:由等比数列的性质可得若{an}成等比数列,Sn是前n项和,则S4,S8-S4,S12-S8成等比数列,故①正确;
若函数y=2sin(ωx+θ)为偶函数(0<θ<π),则θ的值为 ,若其图象与直线y=2的交点的横坐标为x1、x2,若|x1-x2|的最小值为π,则ω的值不一定为2,故②错误;
,若其图象与直线y=2的交点的横坐标为x1、x2,若|x1-x2|的最小值为π,则ω的值不一定为2,故②错误;
第一象限不是一个区间,故③正弦函数在第一象限为单调递增函数错误;
函数y=2sin(2x- )的图象的对称点坐标为(
)的图象的对称点坐标为( +
+ ,0)(k∈Z),当k=0时为(
,0)(k∈Z),当k=0时为( ,0),故④正确;
,0),故④正确;
故答案为:①④
点评:本题考查的知识点是命题的真假判断与应用,等比数列的性质,正弦函数的奇偶性,正弦函数的单调性及正弦函数的对称性,熟练掌握正弦型函数的性质,及等比数列的性质,是解答本题的关键.
解答:解:由等比数列的性质可得若{an}成等比数列,Sn是前n项和,则S4,S8-S4,S12-S8成等比数列,故①正确;
若函数y=2sin(ωx+θ)为偶函数(0<θ<π),则θ的值为
 ,若其图象与直线y=2的交点的横坐标为x1、x2,若|x1-x2|的最小值为π,则ω的值不一定为2,故②错误;
,若其图象与直线y=2的交点的横坐标为x1、x2,若|x1-x2|的最小值为π,则ω的值不一定为2,故②错误;第一象限不是一个区间,故③正弦函数在第一象限为单调递增函数错误;
函数y=2sin(2x-
 )的图象的对称点坐标为(
)的图象的对称点坐标为( +
+ ,0)(k∈Z),当k=0时为(
,0)(k∈Z),当k=0时为( ,0),故④正确;
,0),故④正确;故答案为:①④
点评:本题考查的知识点是命题的真假判断与应用,等比数列的性质,正弦函数的奇偶性,正弦函数的单调性及正弦函数的对称性,熟练掌握正弦型函数的性质,及等比数列的性质,是解答本题的关键.

练习册系列答案
相关题目

 、
、 ,两个不同平面
,两个不同平面 、
、 ,给出下列命题:
,给出下列命题:
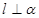 ,则
,则 则
则 在平面
在平面 。
。 ,对任意
,对任意 ,运算“
,运算“ ”具有如下性质:
”具有如下性质: ; (2)
; (2) ; (3)
; (3) .
. :
: ,则
,则 ;
; ,且
,且 ,则a = 0;
,则a = 0; ,且
,且 ,
, ,则a = c.
,则a = c. 和
和 为不重合的两个平面,给出下列命题:1若
为不重合的两个平面,给出下列命题:1若 与
与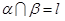 ,若
,若 ;4直线
;4直线 的充要条件是
的充要条件是 、
、 ,且m⊥
,且m⊥ ,
,