题目内容
己知f(x)为定义域为 R 内的减函数,且f(x)=
,则实数a的取值范围为
|
|
[
,
)
| 1 |
| 6 |
| 1 |
| 2 |
[
,
)
.| 1 |
| 6 |
| 1 |
| 2 |
分析:根据对数函数在区间[1,+∞)是减函数得a∈(0,1),由一次函数f(x)=(2a-1)x+4a在区间(-∞,1)是减函数,得到a<
,再根据不等式(2a-1)x+4a≥logax在x=1时成立解出a≥
,最后将各种情况取交集即得实数a的取值范围.
| 1 |
| 2 |
| 1 |
| 6 |
解答:解:∵f(x)为定义域为R内的减函数,
∴当x∈[1,+∞)时,f(x)=logax是减函数,可得a∈(0,1)
当x∈(-∞,1)时,f(x)=(2a-1)x+4a是减函数,得2a-1<0,解之得a<
因此,a的取值范围为(0,
)
又∵(2a-1)x+4a≥logax在x=1时成立
∴(2a-1)×1+4a≥loga1=0,解之得a≥
综上所述,满足条件的实数a的取值范围为[
,
).
故答案为:[
,
)
∴当x∈[1,+∞)时,f(x)=logax是减函数,可得a∈(0,1)
当x∈(-∞,1)时,f(x)=(2a-1)x+4a是减函数,得2a-1<0,解之得a<
| 1 |
| 2 |
因此,a的取值范围为(0,
| 1 |
| 2 |
又∵(2a-1)x+4a≥logax在x=1时成立
∴(2a-1)×1+4a≥loga1=0,解之得a≥
| 1 |
| 6 |
综上所述,满足条件的实数a的取值范围为[
| 1 |
| 6 |
| 1 |
| 2 |
故答案为:[
| 1 |
| 6 |
| 1 |
| 2 |
点评:本题给出分段函数,在已知函数在R上为减函数的情况下求参数a的取值范围,着重考查了基本实数函数的单调性和分段函数单调性的处理等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
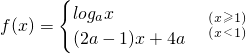 ,则实数a的取值范围为________.
,则实数a的取值范围为________.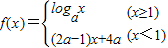 ,则实数a的取值范围为 .
,则实数a的取值范围为 .