题目内容
己知f(x)是定义域为(-1,1)的奇函数,而且f(x)是减函数,如果f(m-2)+f(2m-3)>0,那么实数m的取值范围是 .
【答案】分析:先根据奇函数的性质将不等式f(m-2)+f(2m-3)>0变为f(m-2)>f(3-2m),再由f(x)是定义域为(-1,1)的减函数转化为不等式组,即可解出参数的取值范围
解答:解:由题意(x)是定义域为(-1,1)的奇函数,故不等式f(m-2)+f(2m-3)>0变为f(m-2)>-f(2m-3)=f(3-2m),
又f(x)是减函数故有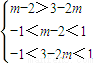 解得1<m<
解得1<m<
故答案为1<m<
点评:本题考查奇偶性与单调性的综合,求解本题的关键有二,一是根据奇函数的性质将不等式变为f(m-2)>f(3-2m),二是通过函数的单调性将抽象不等式变为等价的不等式组,在此过程中易忽视定义域 的要求只得出m-2>3-2m面导致错误,转化时一定要考虑周详,转化要等价.
解答:解:由题意(x)是定义域为(-1,1)的奇函数,故不等式f(m-2)+f(2m-3)>0变为f(m-2)>-f(2m-3)=f(3-2m),
又f(x)是减函数故有
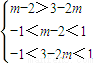 解得1<m<
解得1<m<
故答案为1<m<

点评:本题考查奇偶性与单调性的综合,求解本题的关键有二,一是根据奇函数的性质将不等式变为f(m-2)>f(3-2m),二是通过函数的单调性将抽象不等式变为等价的不等式组,在此过程中易忽视定义域 的要求只得出m-2>3-2m面导致错误,转化时一定要考虑周详,转化要等价.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目