题目内容
 已知A是圆x2+y2=4上任一点,AB垂直于x轴,交x轴于点B.以A为圆心、AB为半径作圆交已知圆于C、D,连接CD交AB于点P,求点P的轨迹方程.
已知A是圆x2+y2=4上任一点,AB垂直于x轴,交x轴于点B.以A为圆心、AB为半径作圆交已知圆于C、D,连接CD交AB于点P,求点P的轨迹方程.分析:设点A的坐标为A(2cosα,2sinα),由以A为圆心、AB为半径的圆的方程及已知圆x2+y2=4的方程,求得公共弦CD的方程,再与AB的方程联立得到点P的坐标为(2cosα,sinα),消去α,由此能求出点Q的轨迹方程.
解答:解:设点A的坐标为A(2cosα,2sinα),则以A为圆心、AB为半径的圆的方程为:
(x-2cosα)2+(y-2sinα)2=4sin2α.
联立已知圆x2+y2=4的方程,相减,可得公共弦CD的方程为:
xcosα+ysinα=1+cos2α. (1)
而AB的方程是 x=2cosα. (2)
所以满足(1)、(2)的点P的坐标为(2cosα,sinα),消去α,即得
点P的轨迹方程为x2+4y2=4.
(x-2cosα)2+(y-2sinα)2=4sin2α.
联立已知圆x2+y2=4的方程,相减,可得公共弦CD的方程为:
xcosα+ysinα=1+cos2α. (1)
而AB的方程是 x=2cosα. (2)
所以满足(1)、(2)的点P的坐标为(2cosα,sinα),消去α,即得
点P的轨迹方程为x2+4y2=4.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆的相关知识,解题时要注意合理地利用参数进行等价转化.

练习册系列答案
相关题目
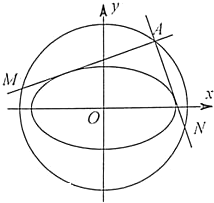 (2013•绍兴一模)已知A是圆x2+y2=4上的一个动点,过点A作两条直线l1,l2,它们与椭圆
(2013•绍兴一模)已知A是圆x2+y2=4上的一个动点,过点A作两条直线l1,l2,它们与椭圆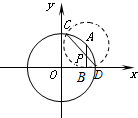 已知A是圆x2+y2=4上任一点,AB垂直于x轴,交x轴于点B.以A为圆心、AB为半径作圆交已知圆于C、D,连接CD交AB于点P,求点P的轨迹方程.
已知A是圆x2+y2=4上任一点,AB垂直于x轴,交x轴于点B.以A为圆心、AB为半径作圆交已知圆于C、D,连接CD交AB于点P,求点P的轨迹方程.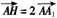 。
。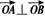 的点,其中O是坐标原点,过点B也作x轴的垂线段,交轨迹C于点B1,动点P满足
的点,其中O是坐标原点,过点B也作x轴的垂线段,交轨迹C于点B1,动点P满足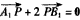 ,求点P的轨迹D的方程;
,求点P的轨迹D的方程;