题目内容
（本小题满分12分）如图，四棱锥P-ABCD中，PA⊥平面ABCD，PA＝AB＝BC＝2，E为PA的中点，过E作平行于底面的平面EFGH，分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形，AD∥BC，AB⊥AD，∠BCD=135°.
（1） 求异面直线AF与BG所成的角的大小；
（2） 求平面APB与平面CPD所成的锐二面角的大小.
(Ⅰ) 
(Ⅱ) 
解析:
解：由题意可知：
两两垂直，可建立空间直角坐标系
。由平面几何知识知：
，
，
， 
，
，
，
，
。
（Ⅰ）
与
所成的角为 ……4分
（Ⅱ）可证明
平面
，
平面的法向量为
.设平面
的法向量为
，
由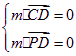
.
平面与平面所成的锐二面角的大小为 6分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
