题目内容
10．设平面区域D是不等式组$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{2x-y-3≤0}\end{array}\right.$的解集，将D绕直线x-y=0旋转一周后所得几何体的体积等于（ ）| A． | $\frac{4\sqrt{2}}{3}$π | B． | $\sqrt{2}$π | C． | 2$\sqrt{2}$π | D． | 3$\sqrt{2}$π |
分析 根据线性规划知识作出符合题意的平面区域为D，再想象出所得旋转体的结构特征，根据题意和图求出旋转体的几何元素的长度，再求出它的体积．
解答 解：在坐标系中画出平面区域为D如下图中阴影部分（OBC）
阴影部分绕直线x-y=0旋转一周后所得几何体为圆锥，
由图得C（3，3），B（1，-1），
则圆锥底面半径OB=$\sqrt{2}$，高OC=$3\sqrt{2}$
则圆锥的体积为$\frac{1}{3}$π（$\sqrt{2}$）2×$3\sqrt{2}$=2$\sqrt{2}$π，
故选：C
点评 本题是综合题，关键利用线性规划知识正确作图，并能想象出所得旋转体为圆锥，再求它的体积．
练习册系列答案
阅读快车系列答案
相关题目
20．已知函数f（x）=x3+bx2+cx的图象如图所示，则x1•x2等于（ ）
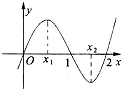
| A． | 2 | B． | $\frac{4}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |
1．设集合M满足{1，2}⊆M?{1，2，3，4}，则满足条件的集合M的个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
18．已知函数f（x）=xlnx，g（x）=ax3-$\frac{1}{2}$x-$\frac{2}{3e}$，若函数f（x）的图象与函数g（x）的图象在交点处存在公切线，则函数g（x）在（1，g（1））处的切线在y轴上的截距为（ ）
| A． | -$\frac{2}{3e}$ | B． | $\frac{2}{3e}$ | C． | -$\frac{{e}^{3}+2}{3e}$ | D． | $\frac{{e}^{2}+2}{3e}$ |
5．
已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，将函数f（x）的图象向左平移m（m＞0）个单位后，得到函数g（x）的图象关于点（$\frac{π}{3}$，$\frac{\sqrt{3}}{2}$）对称，则m的值可能为（ ）
已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，将函数f（x）的图象向左平移m（m＞0）个单位后，得到函数g（x）的图象关于点（$\frac{π}{3}$，$\frac{\sqrt{3}}{2}$）对称，则m的值可能为（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{2}$ | C． | $\frac{7π}{6}$ | D． | $\frac{7π}{12}$ |
3．命题：“正数m的平方等于0”的否命题为（ ）
| A． | 正数m的平方不等于0 | B． | 若m不是正数，则它的平方等于0 | ||
| C． | 若m不是正数，则它的平方不等于0 | D． | 非正数m的平方等于0 |