题目内容
在△ABC中,内角A、B、C的对边分别是a、b、c,若 ,
, ,则A=( )
,则A=( )
| A.30° | B.60° |
| C.120° | D.150° |
A
解析试题分析:因为, ,所以,由正弦定理得
,所以,由正弦定理得 ,又
,又 ,
,
所以, ,
,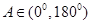 ,
,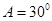 ,选A.
,选A.
考点:正弦定理、余弦定理的应用

练习册系列答案
相关题目
已知△ABC的周长为 ,且
,且 .若△ABC的面积为
.若△ABC的面积为 ,则角C的大小为( )
,则角C的大小为( )
| A.30° | B.60° | C.90° | D.120° |
在 中,如果
中,如果 ,
, =4,
=4, =4,则此三角形有( )
=4,则此三角形有( )
| A.两解 | B.一解 | C.无解 | D.无穷多解 |
已知 中,
中, 分别是内角
分别是内角 所对的边,且
所对的边,且 ,则下列结论正确的是
,则下列结论正确的是
A. | B. | C. | D. |
在 中,
中, ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高是( )
| A.10m |
B.10 m m |
C.10 m m |
D.10 m m |
△ABC的三个内角A,B,C的对边分别a,b,c,且acos C,bcos B,ccos A成等差数列,则角B等于( )
| A.30° | B.60° | C.90° | D.120° |
 ABC中,若cos2A=cos2B,则
ABC中,若cos2A=cos2B,则 ,若
,若 ,则
,则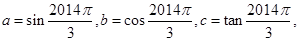 则
则
 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 =2cos(3x+
=2cos(3x+


