题目内容

5．若等比数列{an}，满足a2+a4=40，a3+a5=80，则公比q=2，前n项和Sn=2n+2-4．

分析 由题意易得数列的公比，进而可得首项，由求和公式可得答案．

解答 解：∵等比数列{an}中a2+a4=40，a3+a5=80，
∴数列的公比q=$\frac{{a}_{3}+{a}_{5}}{{a}_{2}+{a}_{4}}$=$\frac{80}{40}$=2，
∴a2+a4=a1（2+8）=40，解得a1=4，
∴前n项和Sn=$\frac{4（1-{2}^{n}）}{1-2}$=2n+2-4，
故答案为：2；2n+2-4．

点评 本题考查等比数列的通项公式和求和公式，属基础题．

练习册系列答案
相关题目
12．不等式（$\frac{1}{3}$）1-x＜7的解集为（-∞，log321）．
16．已知曲线y=2x2-7．
（1）求曲线在点P（3，11）处的切线方程；
（2）求曲线过点P（3，9）的切线方程；
（3）求斜率为4的曲线的切线方程．
13．若数列$\sqrt{2}$，$\sqrt{5}$，2$\sqrt{2}$，…，则2$\sqrt{5}$是这个数列的第（　　）项．
A．6B．7C．8D．9
20．函数f（x）=loga（x-1）+4（a＞0，且a≠1）的图象过定点（2，4）已知幂函数f（x）=xm的图象经过点（4，2），则f（16）=4．
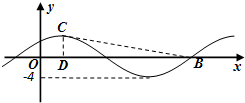
10．已知函数f（x）=Asin（$\frac{1}{2}$x+φ），x∈R（其中ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．设点C（$\frac{2π}{3}$，4）是图象上y轴右侧的第一个最高点，CD⊥DB，则△BDC的面积是（　　）
A．3B．4πC．6πD．12π
17．已知平面a和直线l，则a内至少有一条直线与l（　　）
A．平行B．相交C．垂直D．异面
14．已知数列{an}是公差不为零的等差数列，a1=2，且a2，a4，a8成等比数列，数列{bn}的前n项和为Tn，且Tn=2bn-2（n∈N*）．
（1）求数列{an}的前n项和Sn；
（2）求数列{bn}的通项公式；
（3）记集合M={n|$\frac{{S}_{n}}{{b}_{n}}$≥λ，n∈N*}，若集合M中有且仅有4个元素，求实数λ的取值范围．
15．抛掷两枚骰子，设出现的点数之和是12，11，10的概率依次是P（A），P（B），P（C），则（　　）
A．P（A）=P（B）＜P（C）B．P（A）＜P（B）＜P（C）C．P（A）＜P（B）=P（C）D．P（C）=P（B）＜P（A）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网