题目内容
18.命题“?x∈R,ax2-2ax+3>0恒成立”是假命题,则a的取值范围是(-∞,0)∪[3,+∞).分析 将条件转化为“?x∈R,ax2-2ax+3≤0成立,检验a=0是否满足条件,当a≠0 时,必须a<0或$\left\{\begin{array}{l}{a>0}\\{4{a}^{2}-12a≥0}\end{array}\right.$,从而解出实数a的取值范围.
解答 解:命题“ax2-2ax+3>0恒成立”是假命题,即“?x∈R,ax2-2ax+3≤0成立”是真命题 ①.
当a=0时,①不成立,
当a≠0 时,要使①成立,必须a<0或$\left\{\begin{array}{l}{a>0}\\{4{a}^{2}-12a≥0}\end{array}\right.$,
∴a<0或a≥3
故答案为:(-∞,0)∪[3,+∞).
点评 本题考查一元二次不等式的应用,注意联系对应的二次函数的图象特征,体现了等价转化和分类讨论的数学思想.

练习册系列答案
相关题目
9.定义在R上的偶函数f(x)在[0,+∞)上是增函数,且f($\frac{1}{3}$)=0,则不等式f(log${\;}_{\frac{1}{8}}$x)>0的解是( )
| A. | ($\frac{1}{2}$,1 ) | B. | ( 2,+∞) | C. | ( 0,$\frac{1}{2}$)∪( 2,+∞) | D. | ($\frac{1}{2}$,1 )∪( 2,+∞) |
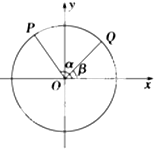 如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于P,Q两点,已知点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$
如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于P,Q两点,已知点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$