题目内容
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别是A1B1和BB1的中点,那么直线AM与CN所成角的余弦值为________.
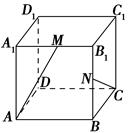

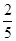
以D为坐标原点,DA为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,则A(1,0,0),M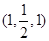 ,C(0,1,0),N
,C(0,1,0),N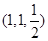 .则
.则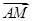 =
=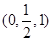 ,
,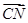 =
=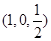 ,
,
∴cos〈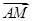 ,
,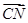 〉=
〉=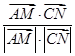 =
=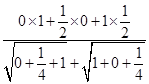 =
=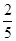 .
.
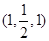 ,C(0,1,0),N
,C(0,1,0),N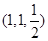 .则
.则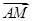 =
=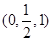 ,
,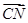 =
=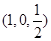 ,
,∴cos〈
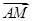 ,
,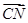 〉=
〉=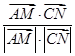 =
=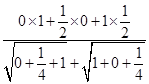 =
=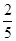 .
.
练习册系列答案
相关题目
题目内容

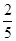
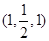 ,C(0,1,0),N
,C(0,1,0),N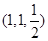 .则
.则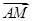 =
=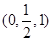 ,
,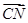 =
=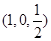 ,
,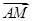 ,
,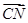 〉=
〉=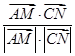 =
=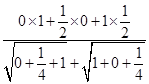 =
=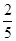 .
.