题目内容
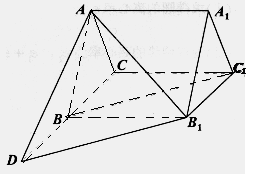
如图,在四棱锥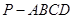 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱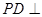 底面ABCD,
底面ABCD,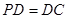 ,E是PC的中点,作
,E是PC的中点,作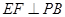 交PB于点F.
交PB于点F.
(1)证明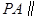 平面
平面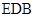 ;
;
(2)证明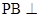 平面EFD;
平面EFD;
(3)求二面角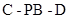 的大小.
的大小.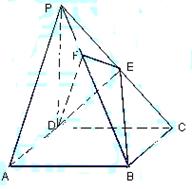
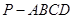 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱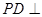 底面ABCD,
底面ABCD,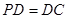 ,E是PC的中点,作
,E是PC的中点,作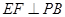 交PB于点F.
交PB于点F.(1)证明
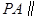 平面
平面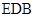 ;
;(2)证明
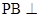 平面EFD;
平面EFD;(3)求二面角
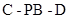 的大小.
的大小.
(1)略 (2)略 (3)

解:如图所示建立空间直角坐标系,D为坐标原点.设
 (1)证明:连结AC,AC交BD于G.连结EG.
(1)证明:连结AC,AC交BD于G.连结EG. 
依题意得

 底面ABCD是正方形,
底面ABCD是正方形,  是此正方形的中心,
是此正方形的中心,故点G的坐标为
 且
且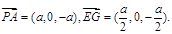
 . 这表明
. 这表明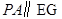 .而
.而 平面EDB且
平面EDB且 平面EDB,
平面EDB, 平面EDB。
平面EDB。(2)证明:依题意得
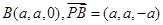 。又
。又 故
故
 , 由已知
, 由已知 ,且
,且 所以
所以 平面EFD.
平面EFD.(3)解:设点F的坐标为
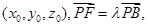 则
则
从而
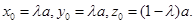 所以
所以
由条件
 知,
知,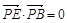 即
即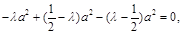 解得
解得 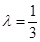 。
。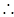 点F的坐标为
点F的坐标为 且
且
 ,即
,即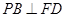 ,故
,故 是二面角
是二面角 的平面角.
的平面角.∵
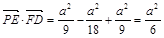 且
且

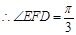 ,所以,二面角C—PC—D的大小为
,所以,二面角C—PC—D的大小为
本试题主要考查了立体几何中线面平行的判定,线面垂直的判定,以及二面角的求解的综合运用试题。体现了运用向量求解立体几何的代数手法的好处。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 中,
中,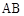
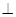 平面
平面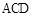 ,
,
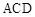 ,
,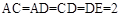 ,
, 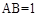 ,
,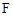 为
为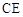 的中点
的中点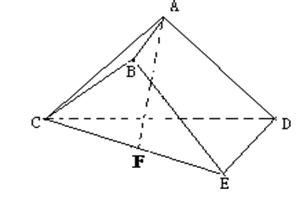
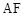
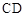 ;
;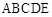 的体积.
的体积.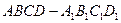 的棱长为
的棱长为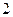 ,
,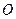 是
是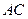 与
与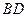 的交点,
的交点,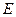 是
是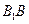 上一点,且
上一点,且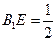 .(Ⅰ)求证:
.(Ⅰ)求证: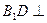 平面
平面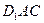 ;
;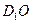 与
与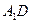 所成角的余弦值;
所成角的余弦值;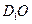 与平面
与平面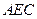 所成角的正弦值.
所成角的正弦值.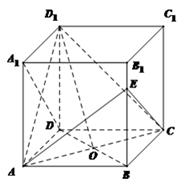
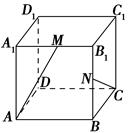
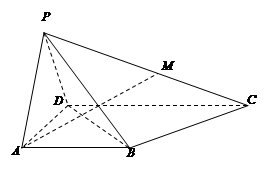
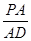 多大时,AM⊥平面PDB可能成立?
多大时,AM⊥平面PDB可能成立?
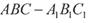 的侧棱与底面垂直,
的侧棱与底面垂直,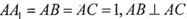 ,MN分别是
,MN分别是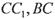 的中点,P点在
的中点,P点在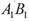 上,且满足
上,且满足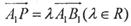
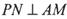
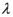 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角 最大?并求出该最大角的正切值;
最大?并求出该最大角的正切值;
 中,
中, 平面
平面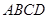 ,底面
,底面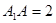 ,
,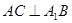 ;
;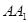 上存在一点
上存在一点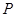 ,使得
,使得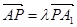 ,
,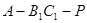 的大小为
的大小为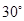 时,求实数
时,求实数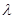 的值.
的值.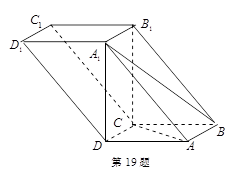
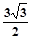 ,D是CB延长线上一点,且BD=BC.
,D是CB延长线上一点,且BD=BC.