题目内容
如图,已知椭圆 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线l交x轴于点K,左顶点为A.
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线l交x轴于点K,左顶点为A.(1)求证:KF平分∠MKN;
(2)直线AM、AN分别交准线l于点P、Q,设直线MN的倾斜角为θ,试用θ表示线段PQ的长度|PQ|,并求|PQ|的最小值.

【答案】分析:(1)法一:几何法,分别过M和N点作准线的垂线,并设出对应的垂足,根据直角梯形列出比例关系,再由椭圆的第二定义,将到焦点的距离之比转化到对应准线的距离之比,判断出∠KMM1=∠KNN1,再由内错角相等得到∠MKF=∠NKF,即得到证明;
法二:代数法,根据题意设直线MN的方程为x=my+1,再设出点M、N的坐标,联立直线和椭圆的方程,消去x得到关于y的一个二次方程,根据韦达定理表示出y1+y2和y1y2,再代入斜率公式,进行证明;
(2)由题意求出点A和右准线的方程,并设出四点M、N、P和Q的坐标,根据A,M,P三点共线得到对应的斜率相等,求出点P和Q的坐标,联立直线和椭圆的方程,消去x得到关于y的一个二次方程,根据韦达定理表示出y1+y2和y1y2,再代入两点之间的距离公式,化简后用m表示|PQ|,再把m用cotθ表示,利用三角恒等变换公式和θ∈(0,π),求出最小值.
解答:解:(1)法一:作MM1⊥l于M1,
NN1⊥l于N1,则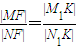 ,
,
由椭圆的第二定义,有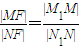 ,
,
∴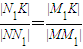 ,
,
∴∠KMM1=∠KNN1,即∠MKF=∠NKF,
∴KF平分∠MKN.
法二:设直线MN的方程为x=my+1,
设M、N的坐标分别为(x1,y1),(x2,y2),
由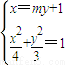 得,(3m2+4)y2+6my-9=0,
得,(3m2+4)y2+6my-9=0,
∴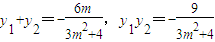
设KM和KN的斜率分别为k1,k2,显然只需证k1+k2=0即可.
∵K(4,0),∴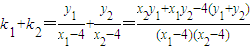
而x2y1+x1y2-4(y1+y2)=(my2+1)y1+(my1+1)y2-4(y1+y2)
=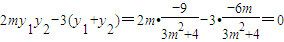 ,
,
即k1+k2=0得证,故KF平分∠MKN.
(2)设M、N的坐标分别为(x1,y1),(x2,y2),
由题意知,A(-2,0),右准线的方程:x=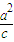 =4,
=4,
故令P(4,yp),Q(4,yq),
∵A,M,P三点共线,∴kAP=kAM,即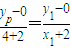 ,得yp=
,得yp=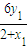 ,即P点为
,即P点为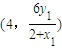
由A,N,Q三点共线,同理可求出Q点为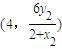 ,
,
设直线MN的方程为x=my+1.由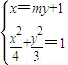 得,(3m2+4)y2+6my-9=0,
得,(3m2+4)y2+6my-9=0,
∴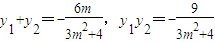 ,
,
则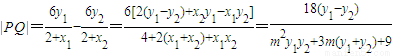
=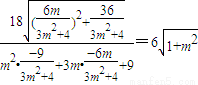
又∵直线MN的倾斜角为θ,则m=cotθ,θ∈(0,π),
∴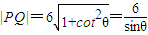 ,
,
∴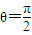 时,|PQ|min=6.
时,|PQ|min=6.
点评:本题主要考查了直线与椭圆的综合问题,两点间的距离公式等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查了学生解决问题的能力和运算能力.
法二:代数法,根据题意设直线MN的方程为x=my+1,再设出点M、N的坐标,联立直线和椭圆的方程,消去x得到关于y的一个二次方程,根据韦达定理表示出y1+y2和y1y2,再代入斜率公式,进行证明;
(2)由题意求出点A和右准线的方程,并设出四点M、N、P和Q的坐标,根据A,M,P三点共线得到对应的斜率相等,求出点P和Q的坐标,联立直线和椭圆的方程,消去x得到关于y的一个二次方程,根据韦达定理表示出y1+y2和y1y2,再代入两点之间的距离公式,化简后用m表示|PQ|,再把m用cotθ表示,利用三角恒等变换公式和θ∈(0,π),求出最小值.
解答:解:(1)法一:作MM1⊥l于M1,

NN1⊥l于N1,则
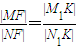 ,
,由椭圆的第二定义,有
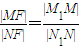 ,
,∴
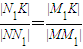 ,
,∴∠KMM1=∠KNN1,即∠MKF=∠NKF,
∴KF平分∠MKN.
法二:设直线MN的方程为x=my+1,
设M、N的坐标分别为(x1,y1),(x2,y2),
由
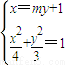 得,(3m2+4)y2+6my-9=0,
得,(3m2+4)y2+6my-9=0,∴
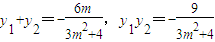
设KM和KN的斜率分别为k1,k2,显然只需证k1+k2=0即可.
∵K(4,0),∴
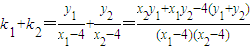
而x2y1+x1y2-4(y1+y2)=(my2+1)y1+(my1+1)y2-4(y1+y2)
=
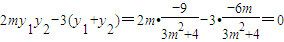 ,
,即k1+k2=0得证,故KF平分∠MKN.
(2)设M、N的坐标分别为(x1,y1),(x2,y2),
由题意知,A(-2,0),右准线的方程:x=
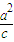 =4,
=4,故令P(4,yp),Q(4,yq),
∵A,M,P三点共线,∴kAP=kAM,即
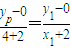 ,得yp=
,得yp=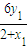 ,即P点为
,即P点为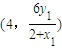
由A,N,Q三点共线,同理可求出Q点为
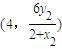 ,
,设直线MN的方程为x=my+1.由
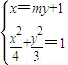 得,(3m2+4)y2+6my-9=0,
得,(3m2+4)y2+6my-9=0,∴
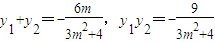 ,
,则
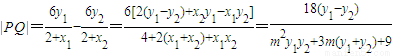
=
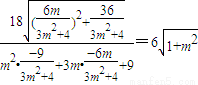
又∵直线MN的倾斜角为θ,则m=cotθ,θ∈(0,π),
∴
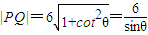 ,
,∴
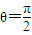 时,|PQ|min=6.
时,|PQ|min=6.点评:本题主要考查了直线与椭圆的综合问题,两点间的距离公式等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查了学生解决问题的能力和运算能力.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:


