题目内容
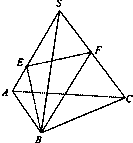
 如图,正三棱锥S-ABC的侧面是边长为a的正三角形,D是SA的中点,E是BC的中点,求△SDE绕直线SE旋转一周所得到的旋转体的体积.
如图,正三棱锥S-ABC的侧面是边长为a的正三角形,D是SA的中点,E是BC的中点,求△SDE绕直线SE旋转一周所得到的旋转体的体积.
分析:连接AE,说明ED⊥SA,作DF⊥SE,交SE于点F.所求的旋转体的体积是以DF为底面半径,分别以SF和EF为高的两个圆锥的体积的和,求出DF,然后求出几何体的体积.
解答:解:连接AE,因为△SDE和△ABC都是边长为a的正三角形,并且SE和AE分别是它们的中线,
所以SE=AE,从而△SEA为等腰三角形,由于D是SA的中点,
所以ED⊥SA.作DF⊥SE,交SE于点F.考虑直角△SDE的面积,得到
SE•DF=
SD•DE,所以,DF=
=
.易知,SE=
=
=
a,
DE=
=
=
a,所以,DF=
•
=
a.
所求的旋转体的体积是以DF为底面半径,分别以SF和EF为高的两个圆锥的体积的和,即
π•(
a)2•SF+
π•(
a)2•EF=
π•(
a)2•SE=
π•
•
a=
πa3.

所以SE=AE,从而△SEA为等腰三角形,由于D是SA的中点,
所以ED⊥SA.作DF⊥SE,交SE于点F.考虑直角△SDE的面积,得到
| 1 |
| 2 |
| 1 |
| 2 |
| SD•DE |
| SE |
| ||
| SE |
| SB2-BE2 |
a2-(
|
| ||
| 2 |
DE=
| SE2-SD2 |
|
| ||
| 2 |
| a |
| 2 |
| ||||
|
| ||
| 6 |
所求的旋转体的体积是以DF为底面半径,分别以SF和EF为高的两个圆锥的体积的和,即
| 1 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| a2 |
| 6 |
| ||
| 2 |
| ||
| 36 |
点评:本题是基础题,考查空间想象能力,圆锥的体积的求法,考查计算能力以及发现问题解决问题的能力.

练习册系列答案
相关题目
 如图,正三棱锥S-ABC中,侧面SAB与底面ABC所成的二面角等于α,动点P在侧面SAB内,PQ⊥底面ABC,垂足为Q,PQ=PS•sinα,则动点P的轨迹为( )
如图,正三棱锥S-ABC中,侧面SAB与底面ABC所成的二面角等于α,动点P在侧面SAB内,PQ⊥底面ABC,垂足为Q,PQ=PS•sinα,则动点P的轨迹为( )| A、线段 | B、圆 | C、一段圆弧 | D、一段抛物线 |
 如图,正三棱锥S-ABC中,∠BSC=40°,SB=2,一质点自点B出发,沿着三棱锥的侧面绕行一周回到点B的最短路线的长为( )
如图,正三棱锥S-ABC中,∠BSC=40°,SB=2,一质点自点B出发,沿着三棱锥的侧面绕行一周回到点B的最短路线的长为( ) 如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.
如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.