题目内容
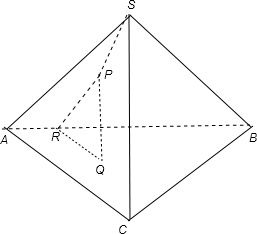
如图，正三棱锥S-ABC中，侧面SAB与底面ABC所成的二面角等于α，动点P在侧面SAB内，PQ⊥底面ABC，垂足为Q，PQ=PS•sinα，则动点P的轨迹为（ ）| A、线段 | B、圆 | C、一段圆弧 | D、一段抛物线 |
分析：构造一个直角三角形PRQ，使∠PRQ为侧面SAB与底面ABC所成的二面角α，直角三角形PRQ中，sinα=
，由已知得
sinα=
，得到PS=PR，即点P到点S的距离等于点P到AB的距离，由抛物线的定义得出结论．
| PQ |
| PR |
sinα=
| PQ |
| PS |
解答：解：如图：过点P作AB得垂线段PR，连接RQ，则RQ是PR在面ABC内的射影，由三垂线定理得逆定理得，OR⊥AB，
∠PRQ为侧面SAB与底面ABC所成的二面角α，直角三角形PRQ中，sinα=
，又已知 PQ=PS•sinα，
∴sinα=
，∴
=
，∴PS=PR，即点P到点S的距离等于点P到AB的距离，
根据抛物线的定义，点P在以点S为焦点，以AB为准线的抛物线上．又点P在侧面SAB内，故点P的轨迹为
一段抛物线，故选 D．
∠PRQ为侧面SAB与底面ABC所成的二面角α，直角三角形PRQ中，sinα=
| PQ |
| PR |
∴sinα=
| PQ |
| PS |
| PQ |
| PR |
| PQ |
| PS |
根据抛物线的定义，点P在以点S为焦点，以AB为准线的抛物线上．又点P在侧面SAB内，故点P的轨迹为
一段抛物线，故选 D．
点评：本题考查二面角的平面角的求法，直角三角形中的边角关系，以及抛物线的定义得应用．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
相关题目
如图，正三棱锥S-ABC的侧面是边长为a的正三角形，D是SA的中点，E是BC的中点，求△SDE绕直线SE旋转一周所得到的旋转体的体积．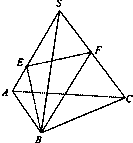
如图，正三棱锥S-ABC中，∠BSC=40°，SB=2，一质点自点B出发，沿着三棱锥的侧面绕行一周回到点B的最短路线的长为（ ）
如图，正三棱锥S-ABC中，底面的边长是3，棱锥的侧面积等于底面积的2倍，M是BC的中点．
B.
或
D.
或