Question

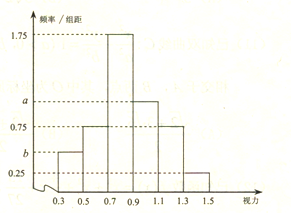
【题目】从某校高三年级中随机抽取100名学生，对其高校招生体检表中的视图情况进行统计，得到如图所示的频率分布直方图，已知从这100人中随机抽取1人，其视力在的概率为.

（1）求的值；

（2）若某大学专业的报考要求之一是视力在0.9以上，则对这100人中能报考专业的学生采用按视力分层抽样的方法抽取8人，调查他们对专业的了解程度，现从这8人中随机抽取3人进行是否有意向报考该大学专业的调查，记抽到的学生中视力在的人数为，求的分布列及数学期望.

Answer 1

【答案】（1）,（2）见解析

【解析】分析：(1)先根据小长方形的面积等于对应区间概率得b，再根据所有小长方形面积和为1求区间[0.9,1.1]概率，除以组距即得a,(2)先根据分层抽样得确定视力在的人数为3，再确定随机变量的取法，分别利用组合数求对应概率，列表可得分布列，最后根据数学期望公式求期望.

详解：

解：（1）；

（2）的可能取值为0，1，2，3，

概率为：，

，所以其分布列如下：

	0	1	2	3

则.