题目内容
随机变量ξ的概率分布规律为P（ξ=k）=a（11-2k）（k=1、2、3、4、5），其中a是常数，则P(
＜ξ＜
)的值为（ ）
| 5 |
| 2 |
| 13 |
| 5 |
分析：利用所有概率的和为1，求出a的值，利用P（
＜ξ＜
）=P（ξ=3）+P（ξ=4），可得结论．
| 5 |
| 2 |
| 23 |
| 5 |
解答：解：由题意，由所有概率的和为1可得a（9+7+5+3+1）=1
∴a=
∴P（
＜ξ＜
）=P（ξ=3）+P（ξ=4）=
+
=
故选D．
∴a=
| 1 |
| 25 |
∴P（
| 5 |
| 2 |
| 23 |
| 5 |
| 5 |
| 25 |
| 3 |
| 25 |
| 8 |
| 25 |
故选D．
点评：本题考查概率的计算，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
随机变量X的概率分布规律为P（X=n）=
（n=1，2，3，4），其中a是常数，则P（
＜X＜
）的值为（ ）
| a |
| n(n+1) |
| 1 |
| 2 |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
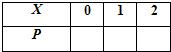从装有3个红球，2个白球的袋中随机取出2个球，设其中有X个红球，则随机变量X的概率分布为