题目内容
7.F1是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,点P是双曲线右支上一点,若线段PF1与y轴的交点M恰为PF1的中点,且|OM|=a(O为坐标原点),则C的离心率为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
分析 由题意,设右焦点是F2,则|PF2|=2a,|PF1|=4a,运用中位线定理和勾股定理可得16a2=4a2+4c2,即可求出双曲线的离心率.
解答 解:由题意,设右焦点是F2,
则|PF2|=2a,|PF1|=4a,
由中位线定理可得,PF2⊥F1F2,
由勾股定理可得16a2=4a2+4c2,
即有3a2=c2,
∴e=$\frac{c}{a}$=$\sqrt{3}$,
故选:B.
点评 本题考查双曲线的离心率,考查勾股定理的运用,确定|PF2|=2a,|PF1|=4a,PF2⊥F1F2,是关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
15.已知向量$\overrightarrow{a}$=(2,4),向量$\overrightarrow{b}$=(x,3),且$\overrightarrow a⊥\overrightarrow b$,则x的值是( )
| A. | 6 | B. | -6 | C. | 9 | D. | 12 |
16.已知f(x)是定义在R上的奇函数,且当x<0时,f(x)=2x,则f(log49)的值为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.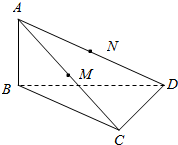 如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.