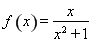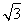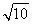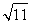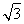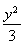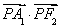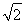题目内容
已知椭圆E: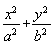 =1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=
=1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=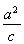 的距离为3.
的距离为3.
(1)求椭圆E的方程;
(2)若存在以原点为圆心的圆,使该圆的任意一条切线与椭圆E恒有两个交点A,B,且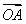 ⊥
⊥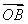 ,求出该圆的方程.
,求出该圆的方程.
(1)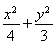 =1(2)x2+y2=
=1(2)x2+y2=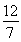
【解析】(1)由题知2|F1F2|=|MF1|+|MF2|,
即2×2c=2a,得a=2c.
又由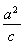 -c=3,解得c=1,a=2,b=
-c=3,解得c=1,a=2,b=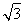 .
.
∴椭圆E的方程为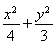 =1.
=1.
(2)假设以原点为圆心,r为半径的圆满足条件.
(ⅰ)若圆的切线的斜率存在,并设其方程为y=kx+m,则r=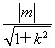 ,r2=
,r2=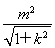 ,①
,①
由 消去y,整理得(3+4k2)x2+8kmx+4(m2-3)=0,设A(x1,y1),B(x2,y2),有
消去y,整理得(3+4k2)x2+8kmx+4(m2-3)=0,设A(x1,y1),B(x2,y2),有
又∵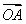 ⊥
⊥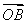 ,∴x1x2+y1y2=0,
,∴x1x2+y1y2=0,
即4(1+k2)(m2-3)-8k2m2+3m2+4k2m2=0,化简得m2=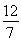 (k2+1),②
(k2+1),②
由①②求得r2=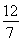 .
.
所求圆的方程为x2+y2=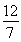 .
.
(ⅱ)若AB的斜率不存在,设A(x1,y1),则B(x1,-y1),∵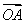 ⊥
⊥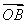 ,∴
,∴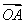 ·
·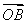 =0,有
=0,有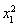 -
-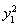 =0,
=0, =
=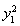 ,代入
,代入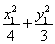 =1,得
=1,得 =
=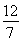 .此时仍有r2=|
.此时仍有r2=|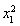 |=
|=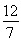 .
.
综上,总存在以原点为圆心的圆x2+y2=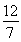 满足题设条件
满足题设条件

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案某校为了研究学生的性别和对待某一活动的态度(支持和不支持的两种态度)的关系,运用2×2列联表进行独立性检验,经计算K2=7.069,则所得到的统计学结论是:有________的把握认为“学生性别与支持该活动有关系”( )
附:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
A.0.1% B.1% C.99% D.99.9%