Question

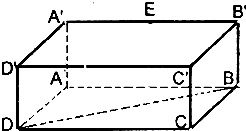已知长方体ABCD-A′B′C′D′，AB=2，AA′=1，直线BD与平面AA′B′B所成角为30°，E为A′B′的中点．
（1）求异面直线AC与BE所成的角；
（2）求A点到平面BDE的距离．

Answer 1

分析：（1）取C′D′在中点O，连接EO，OC，AC，则∠OCA（或其补角）为异面直线AC与BE所成的角，利用余弦定理可求；
（2）利用V_A-BDE=V_D-ABE，可求A点到平面BDE的距离．

解答：解：（1）如图，取C′D′在中点O，连接EO，OC，AC，
∵E为A′B′的中点，
∴四边形EOCB是平行四边形
∴EB∥OC
∴∠OCA（或其补角）为异面直线AC与BE所成的角
∵DA⊥平面AA′B′B，直线BD与平面AA′B′B所成角为30°，
∴∠DBA=30°
∵AB=2，∴AD=

2 3

3

，DB=

4 3

3

△AOC中，OC=

2

，AC=

4 3

3

，AO=

3

∴cos∠OCA=

( 4 3 3 )2+2-3

2• 4 3 3 • 2

=

13 6

48

∴∠COA=arccos

13 6

48

；
（2）设A点到平面BDE的距离为h，则
在△BDE中，BE=

2

，DB=

4 3

3

，DE=

10 3

∴DB²=BE²+DE²
∴S_△BDE=

1

2

×

2

×

10 3

=

60

6

∵S△AEB=

1

2

×2×1=1，V_A-BDE=V_D-ABE
∴

1

3

×

60

6

×h=

1

3

×1×

2 3

3

∴h=

2 5

5

．

点评：本题考查异面直线所成角，考查点到面的距离的计算，考查学生的计算能力，属于中档题．