题目内容
 已知点P是椭圆
已知点P是椭圆| x2 |
| 169 |
| y2 |
| 144 |
(1)求该椭圆的长轴长、右准线方程;
(2)一抛物线以椭圆的中心为顶点、椭圆的右准线为准线,求抛物线标准方程;
(3)当∠F1PF2=30°时,求△PF1F2的面积;
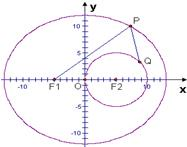
(4)点Q是圆F2:(x-5)2+y2=25上一动点,求PF1+PQ的最小值.
分析:(1)由椭圆
+
=1的标准方程得出a=13,b=12,c=5,从而得到长轴长26,右准线方x=
;
(2)欲求抛物线标准方程,只须求出其焦参数p即可,由
p=
,p=
×2=135.2,最后写出抛物线标准方程;
(3)先设出PF1=r1,PF2=r2,由题意2c=10,利用余弦定理得出r2r1=576(2-
),根据面积公式即可求得△PF1F2的面积;
(4)由于PF1+PQ=26-PF2+PQ=26-(PF2-PQ),故求PF1+PQ的最小值即求PF2-PQ值,由图可知,当三点P,F2,Q共线时,PF2-PQ最大从而得到PF1+PQ的最小值.
| x2 |
| 169 |
| y2 |
| 144 |
| 169 |
| 5 |
(2)欲求抛物线标准方程,只须求出其焦参数p即可,由
| 1 |
| 2 |
| 169 |
| 5 |
| 169 |
| 5 |
(3)先设出PF1=r1,PF2=r2,由题意2c=10,利用余弦定理得出r2r1=576(2-
| 3 |
(4)由于PF1+PQ=26-PF2+PQ=26-(PF2-PQ),故求PF1+PQ的最小值即求PF2-PQ值,由图可知,当三点P,F2,Q共线时,PF2-PQ最大从而得到PF1+PQ的最小值.
解答:解:(1)∵椭圆
+
=1
∴a=13,b=12,c=5,
∴长轴长26,右准线方x=
…(4分)
(2)∵
p=
,p=
×2=67.6
∴抛物线标准方程y2=-135.2x…(8分)
(3)PF1=r1,PF2=r2,由题意2c=10,100=r12+r22-2r1r2cos30°,r1+r2=26..(11分)
∴r2r1=576(2-
)
∴△PF1F2的面积=
r2r1sin30°=144(2-
)…(13分)
(4)由于PF1+PQ=26-PF2+PQ=26-(PF2-PQ)
故求PF1+PQ的最小值即求PF2-PQ值,
由图可知,当三点P,F2,Q共线时,PF2-PQ最大,最大值为圆F2:(x-5)2+y2=25的半径5
故PF1+PQ的最小值为26-5=21…(16分)
| x2 |
| 169 |
| y2 |
| 144 |
∴a=13,b=12,c=5,
∴长轴长26,右准线方x=
| 169 |
| 5 |
(2)∵
| 1 |
| 2 |
| 169 |
| 5 |
| 169 |
| 5 |
∴抛物线标准方程y2=-135.2x…(8分)
(3)PF1=r1,PF2=r2,由题意2c=10,100=r12+r22-2r1r2cos30°,r1+r2=26..(11分)
∴r2r1=576(2-
| 3 |
∴△PF1F2的面积=
| 1 |
| 2 |
| 3 |
(4)由于PF1+PQ=26-PF2+PQ=26-(PF2-PQ)
故求PF1+PQ的最小值即求PF2-PQ值,
由图可知,当三点P,F2,Q共线时,PF2-PQ最大,最大值为圆F2:(x-5)2+y2=25的半径5
故PF1+PQ的最小值为26-5=21…(16分)
点评:本小题主要考查椭圆的简单性质、直线和圆的方程的应用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目