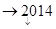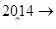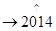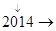题目内容
用数学归纳法证明1＋
＋
＋…＋
>
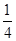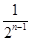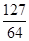(n∈N*)成立，其初始值至少应取( )
| A．7 | B．8 | C．9 | D．10 |
B
解析
练习册系列答案
相关题目
用反证法证明命题“三角形的内角至多有一个钝角”时，假设的内容应为（ ）
| A．假设至少有一个钝角 | B．假设至少有两个钝角 |
| C．假设没有一个钝角 | D．假设没有一个钝角或至少有两个钝角 |
用火柴棒摆“金鱼”，如图所示：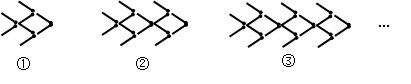
按照上面的规律，第4个“金鱼”图需要火柴棒的根数为
| A．24 | B．26 | C．28 | D．30 |
用反证法证明命题“设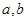
为实数，则方程
至少有一个实根”时，要做的假设是（ ）
| A．方程没有实根 | B．方程至多有一个实根 |
| C．方程至多有两个实根 | D．方程恰好有两个实根 |
分析法又称执果索因法，若用分析法证明：“设a>b>c，且a＋b＋c＝0，求证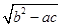 
<
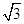a”索的因应是( )
| A．a－b>0 | B．a－c>0 |
| C．(a－b)(a－c)>0 | D．(a－b)(a－c)<0 |
设x，y，z>0，则三个数
＋
，
＋
，
＋
( )
| A．都大于2 | B．至少有一个大于2 |
| C．至少有一个不小于2 | D．至少有一个不大于2 |
如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,那么( )
| A．△A1B1C1和△A2B2C2都是锐角三角形 |
| B．△A1B1C1和△A2B2C2都是钝角三角形 |
| C．△A1B1C1是钝角三角形,△A2B2C2是锐角三角形 |
| D．△A1B1C1是锐角三角形,△A2B2C2是钝角三角形 |