题目内容
20.已知函数y=f(x)为R上的奇函数,且f(x+2)=f(x),当0<x≤1时,f(x)=2x,若常数a∈(3,4],则f(a)=-24-a.分析 确定函数的周期为2,4-a∈[0,1),利用当0<x≤1时,f(x)=2x,即可求得结论.
解答 解:∵f(x+2)=f(x),
∴函数的周期为2,
∵y=f(x)为R上的奇函数,
∴f(a)=f(a-4)=-f(4-a)
∵a∈(3,4],
∴a-4∈(-1,0],
∴4-a∈[0,1)
∵0<x≤1时,f(x)=2x,
∴f(a)=f(a-4)=-f(4-a)=-24-a,
故答案为:-24-a.
点评 本题考查函数的奇偶性、周期性,考查学生转化问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列命题中,既是真命题又是特称命题的是( )
| A. | 有一个α,使tan(90°-α)=$\frac{1}{tanα}$ | |
| B. | 存在实数x,使sinx=$\frac{π}{2}$ | |
| C. | 对一切α,sin(180°-α)=sinα | |
| D. | sin15°=sin60°cos45°-cos60°sin45° |
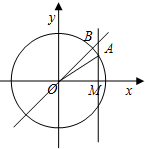 如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A,直线MA垂直x轴于点M,B是直线y=x与MA的交点,设f(α)=$\overrightarrow{OA}•\overrightarrow{OB}$.
如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A,直线MA垂直x轴于点M,B是直线y=x与MA的交点,设f(α)=$\overrightarrow{OA}•\overrightarrow{OB}$.