题目内容
若函数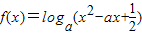 有最小值,则实数a的取值范围是( )
有最小值,则实数a的取值范围是( )A.(0,1)
B.
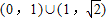
C.
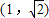
D.
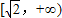
【答案】分析:由题意可知函数取得最小值,须有内函数t=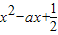 也能取到最值才可以,又因为函数t=
也能取到最值才可以,又因为函数t= 只能取到最小值,因此可得外函数logat的底数a>1,再利用t的最小值须大于0即可解答.
只能取到最小值,因此可得外函数logat的底数a>1,再利用t的最小值须大于0即可解答.
解答:解:设t=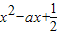 ,则须有t>0成立,
,则须有t>0成立,
要使函数 有最小值,必须使函数y=logat为增函数,即有a>1,
有最小值,必须使函数y=logat为增函数,即有a>1,
又因为t=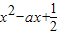 =
= ,
,
所以函数t=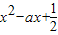 须存在最小值
须存在最小值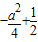 ,且有:
,且有: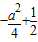 >0,
>0,
于是可得:a2<2,又a>1,即得:1<a<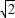 .
.
故应选:C.
点评:本题考查函数的最值,含参数的函数问题的讨论,又考查了复合函数的概念,性质,数形结合,分类讨论思想,配方法等方法的应用.
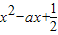 也能取到最值才可以,又因为函数t=
也能取到最值才可以,又因为函数t= 只能取到最小值,因此可得外函数logat的底数a>1,再利用t的最小值须大于0即可解答.
只能取到最小值,因此可得外函数logat的底数a>1,再利用t的最小值须大于0即可解答.解答:解:设t=
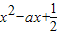 ,则须有t>0成立,
,则须有t>0成立,要使函数
 有最小值,必须使函数y=logat为增函数,即有a>1,
有最小值,必须使函数y=logat为增函数,即有a>1,又因为t=
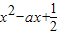 =
= ,
,所以函数t=
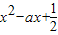 须存在最小值
须存在最小值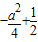 ,且有:
,且有: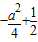 >0,
>0,于是可得:a2<2,又a>1,即得:1<a<
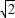 .
.故应选:C.
点评:本题考查函数的最值,含参数的函数问题的讨论,又考查了复合函数的概念,性质,数形结合,分类讨论思想,配方法等方法的应用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 既无最小值也无最大值;
既无最小值也无最大值; 上随机取一个数
上随机取一个数 ,使得
,使得 成立的概率为
成立的概率为 ;
; 对任意正实数
对任意正实数 恒成立,则正实数
恒成立,则正实数 的最小值为16;
的最小值为16; ,若方程
,若方程 恰有三个不同的实根,则实数
恰有三个不同的实根,则实数 的取值范围是
的取值范围是 ;以上正确的命题序号是:_______.
;以上正确的命题序号是:_______.