题目内容
若有下列命题:①|x|2+|x|-2=0有四个实数解;②设a、b、c是实数,若二次方程ax2+bx+c=0无实根,则ac≥0;③若x2-3x+2≠0,则x≠2,④若x∈R,则函数y=| x2+4 |
| 1 | ||
|
(写出所有假命题的序号).
分析:①|x|2+|x|-2=0先求出|x|的取值,从而判定根的个数,即可得到命题的真假;②先根据二次方程ax2+bx+c=0无实根,求出a、b、c的关系,可得到命题的真假;③若x2-3x+2≠0,求出x的范围,可得到命题的真假;④求函数y=
+
的最值时注意
的范围,求出最小值,进行判定真假.
| x2+4 |
| 1 | ||
|
| x2+4 |
解答:解:①|x|2+|x|-2=0则|x|=1或|x|=-2,故方程只有两个实数解,故是假命题;
②设a、b、c是实数,若二次方程ax2+bx+c=0无实根,则b2-4ac<0,则ac>
≥0,则ac≥0,故是真命题;
③若x2-3x+2≠0,则x≠2且x≠1,可推出x≠2,故是真命题;
④若x∈R,则函数y=
+
的最小值为
,此时x=0,故是假命题.
故答案为:①、④
②设a、b、c是实数,若二次方程ax2+bx+c=0无实根,则b2-4ac<0,则ac>
| b2 |
| 4 |
③若x2-3x+2≠0,则x≠2且x≠1,可推出x≠2,故是真命题;
④若x∈R,则函数y=
| x2+4 |
| 1 | ||
|
| 5 |
| 2 |
故答案为:①、④
点评:本题考查一元二次方程的根的分布与系数的关系,命题的真假的判定,函数单调性的应用,考查分析问题解决问题的能力,解决此类问题往往是逐一进行判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
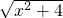 +
+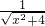 的最小值为2.上述命题中是假命题的有________
的最小值为2.上述命题中是假命题的有________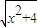 +
+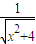 的最小值为2.上述命题中是假命题的有
的最小值为2.上述命题中是假命题的有