题目内容
预计某地区明年从年初开始的前x个月内,对某种商品的需求总量f(x)(万件)近似满足:f(x)=x(x+1)(35-2x)(x∈N*,且x≤12)
(1)写出明年第x个月的需求量g(x)(万件)与月份x的函数关系式,并求出哪个月份的需求量超过192万件;
(2)如果将该商品每月都投放到该地区P万件(不包含积压商品),要保证每月都满足供应,P应至少为多少万件?(积压商品转入下月继续销售)
解:(1)当x=1时,g(1)=f(1)=66(万件)
当x≥2时,g(x)=f(x)-f(x-1)
=x(x+1)(35-2x)-(x-1)x(37-2x)=-6x2+72x.
所以,g(x)=-6(x2-12x)(x∈N*且x≤12).
由g(x)>192,即-6(x2-12x)>192.
化简得x2-12x+32<0,解得4<x<8.
又x∈N*,所以x=5,6,7.
答:第5,6,7月份的需求量超过192万件;
(2)要保证每月都满足供应,则 对于x∈N*,x≤12恒成立.
对于x∈N*,x≤12恒成立.
 .
.
所以当x=8时, 取最大值171.
取最大值171.
所以P≥171.
答:每月至少应投放171万件.
分析:(1)当x=1时直接代入f(x)的解析式求解,当x≥2时,由g(x)=f(x)-f(x-1)列式求解,求出g(x)后直接求解不等式得到满足条件的月份;
(2)由题意可得 对于x∈N*,x≤12恒成立,代入g(x)解析式后利用二次函数求最值,从而得到答案.
对于x∈N*,x≤12恒成立,代入g(x)解析式后利用二次函数求最值,从而得到答案.
点评:本题考查了函数模型的选择及应用,考查了简单的数学建模思想方法,考查了一元二次不等式的解法及二次函数最值的求法,是中档题.
当x≥2时,g(x)=f(x)-f(x-1)
=x(x+1)(35-2x)-(x-1)x(37-2x)=-6x2+72x.
所以,g(x)=-6(x2-12x)(x∈N*且x≤12).
由g(x)>192,即-6(x2-12x)>192.
化简得x2-12x+32<0,解得4<x<8.
又x∈N*,所以x=5,6,7.
答:第5,6,7月份的需求量超过192万件;
(2)要保证每月都满足供应,则
 对于x∈N*,x≤12恒成立.
对于x∈N*,x≤12恒成立. .
.所以当x=8时,
 取最大值171.
取最大值171.所以P≥171.
答:每月至少应投放171万件.
分析:(1)当x=1时直接代入f(x)的解析式求解,当x≥2时,由g(x)=f(x)-f(x-1)列式求解,求出g(x)后直接求解不等式得到满足条件的月份;
(2)由题意可得
 对于x∈N*,x≤12恒成立,代入g(x)解析式后利用二次函数求最值,从而得到答案.
对于x∈N*,x≤12恒成立,代入g(x)解析式后利用二次函数求最值,从而得到答案.点评:本题考查了函数模型的选择及应用,考查了简单的数学建模思想方法,考查了一元二次不等式的解法及二次函数最值的求法,是中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
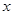 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量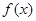 (万件)近似满足:
(万件)近似满足: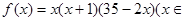 N*,且
N*,且 )
)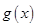 (万件)与月份
(万件)与月份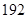 万件;
万件;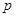 万件(不包含积压商品),要保证每月都满足供应,
万件(不包含积压商品),要保证每月都满足供应,