题目内容
某地区预计明年从年初开始的前x个月内,对某种商品的需求总量f(x)(万件)与月份x的近似关系为:f(x)=
| 1 | 150 |
(1)写出明年第x个月的需求量g(x)(万件)与月x的函数关系,并求出哪个月份的需求量最大,最大需求量是多少?
(2)如果将该商品每月都投放市场p万件(销售未完的商品都可以在以后各月销售),要保证每月都足量供应,问:p至少为多少万件?
分析:(1)把x=1代入到f(x)得到f(1)即为g(1),当x≥2时,g(x)=f(x)-f(x-1)化简得出解析式并求出当x为多少时g(x)的最大值即可;
(2)对一切x∈{1,2,12}有px≥f(x)列出不等式得到P≥一个函数,求出函数的最大值得到P的取值范围.
(2)对一切x∈{1,2,12}有px≥f(x)列出不等式得到P≥一个函数,求出函数的最大值得到P的取值范围.
解答:解:(1)g(1)=f(1)=
×1×2×33=
.
当x≥2时,g(x)=f(x)-f(x-1)=
x(x+1)(35-2x)-
(x-1)x(37-2x)=
x•[(35+33x-2x2)-(-37+39x-2x2)]=
x•(72-6x)=
x•(12-x).
所以:g(x)=
∵g(x)≤
[
]2=
.∴当x=12-x,即x=6时,g(x)max=
(万件).
故6月份该商品需求量最大,最大需求量为
万件.
(2)依题意,对一切x∈{1,2,12}有px≥f(x).
∴p≥
(x+1)(35-2x)(x=1,2,12).
设h(x)=
(35+33x-2x2),
∴h(x)max=h(8)=1.14.故p≥1.14.
故每个月至少投放1.14万件,可以保证每个月都保证供应.
| 1 |
| 150 |
| 11 |
| 25 |
当x≥2时,g(x)=f(x)-f(x-1)=
| 1 |
| 150 |
| 1 |
| 150 |
| 1 |
| 150 |
| 1 |
| 150 |
| 1 |
| 25 |
所以:g(x)=
|
∵g(x)≤
| 1 |
| 25 |
| x+(12-x) |
| 2 |
| 36 |
| 25 |
| 36 |
| 25 |
故6月份该商品需求量最大,最大需求量为
| 36 |
| 25 |
(2)依题意,对一切x∈{1,2,12}有px≥f(x).
∴p≥
| 1 |
| 150 |
设h(x)=
| 1 |
| 150 |
∴h(x)max=h(8)=1.14.故p≥1.14.
故每个月至少投放1.14万件,可以保证每个月都保证供应.
点评:考查学生根据实际问题选择函数类型的能力.理解函数最值及其意义.

练习册系列答案
相关题目
 x(x+1)(35-2x)(x∈N*,且x≤12).
x(x+1)(35-2x)(x∈N*,且x≤12).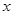 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量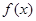 (万件)与月份
(万件)与月份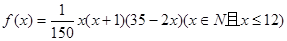 .
.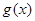 (万件)与月份
(万件)与月份