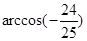题目内容
已知三点A(2,3),B(-1,-1),C(6,k),其中k为常数.若|
|=|
|,则
与
的夹角为( )
| AB |
| AC |
| AB |
| AC |
A、arccos(-
| ||||
B、
| ||||
C、arccos
| ||||
D、
|
分析:根据两个向量的模相等,代入题目所给的坐标,列出关系式,解出K的值,根据点的坐标写出向量的坐标,用向量夹角公式求出夹角的余弦值,得到夹角.
解答:解:∵|
|=|
|
∴k=0或6,
当k=0时,
与
的夹角为
,
当k=6时,
与
的夹角为π-arccos
,
故选D
| AB |
| AC |
∴k=0或6,
当k=0时,
| AB |
| AC |
| π |
| 2 |
当k=6时,
| AB |
| AC |
| 24 |
| 25 |
故选D
点评:本题是对向量数量积的考查,根据两个向量的夹角和模之间的关系,用数量积列出等式,解出未知数,注意要求的结果算出两个,要对着两个结果逐个验证,得到夹角的余弦.

练习册系列答案
相关题目
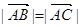 ,则向量
,则向量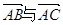 的夹角为(
)
的夹角为(
)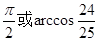 B.
B.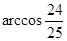
 D.
D.