题目内容
某中学在运动会期间举行定点投篮比赛，规定每人投篮4次，投中一球得2分，没有投中得0分，假设每次投篮投中与否是相互独立的，已知小明每次投篮投中的概率都是
．
（1）求小明在投篮过程中直到第三次才投中的概率；
（2）求小明在4次投篮后的总得分
的分布列和期望．
．（1）求小明在投篮过程中直到第三次才投中的概率；
（2）求小明在4次投篮后的总得分
的分布列和期望．（1）
；（2）
E()=
．
；（2）| ξ | 0 | 2 | 4 | 6 | 8 |
| P |  |  |  |  |  |
E(
)=．试题分析：（1）由于每次投篮投中与否是相互独立的，且知小明每次投篮投中的概率都是
，所以小明在投篮过程中直到第三次才投中则说明他第一次和第二次均未投中，且第三次投中，故由相互独立事件同时发生的概率积公式可求小明在投篮过程中直到第三次才投中的概率；（2）首先由已知确定ξ的所有可能取值应为：0、2、4、6、8，由于每次投篮投中与否是相互独立的，且小明每次投篮投中的概率相等都是，所以小明在4次投篮后的总得分服从参数为４和的二项分布，从而由公式
得到的分布列，再由数学期望公式就可算出
的值．试题解析：（1）设小明在第i次投篮投中为事件Ai（i=1、2、3、4），由已知有
，且事件A1，A2，A3，A4两两相互独立，则小明第三次投篮时首次投中的概率为：
.（2）由已知得ξ的所有可能取值为0、2、4、6、8，则
，所以有：
，
，
，
，
ξ的分布列为
| ξ | 0 | 2 | 4 | 6 | 8 |
| P | | | | | |
∴
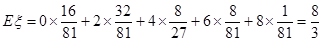
练习册系列答案
相关题目
，在赔付金额为4000元的样本车辆中，车主是新司机的占
，（3）估计在已投保车辆中，新司机获赔金额为4000元的概率.
，“第2次拿出的是白球”为事件
，则事件
，
，点P的坐标为（
，
），
，
，则点P在直线
下方的概率为 .[ 
、
、
、
、
、
六个数字的
