题目内容
三人独立破译同一份密码.已知三人各自破译出密码的概率分别为
,
,
,且他们是否破译出密码互不影响.
(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
记“第i个人破译出密码”为事件A1(i=1,2,3),
依题意有P(A1)=
,P(A2)=
,P(A3)=
,
且A1,A2,A3相互独立.
(Ⅰ)设“恰好二人破译出密码”为事件B,则有
B=A1•A2•
•A1•
•A3+
•A2•A3,
且A1•A2•
,A1•
•A3,
•A2•A3彼此互斥
于是P(B)=P(A1•A2•
)+P(A1•
•A3)+P(
•A2•A3)
=
×
×
+
×
×
+
×
×
=
.
答:恰好二人破译出密码的概率为
.
(Ⅱ)设“密码被破译”为事件C,“密码未被破译”为事件D.
D=
•
•
,且
,
,
互相独立,则有
P(D)=P(
)•P(
)•P(
)=
×
×
=
.
而P(C)=1-P(D)=
,
故P(C)>P(D).
答:密码被破译的概率比密码未被破译的概率大.
依题意有P(A1)=
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| .3 |
且A1,A2,A3相互独立.
(Ⅰ)设“恰好二人破译出密码”为事件B,则有
B=A1•A2•
| . |
| A3 |
| . |
| A2 |
| . |
| A1 |
且A1•A2•
| . |
| A3 |
| . |
| A2 |
| . |
| A1 |
于是P(B)=P(A1•A2•
| . |
| A3 |
| . |
| A2 |
| . |
| A1 |
=
| 1 |
| 5 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
=
| 3 |
| 20 |
答:恰好二人破译出密码的概率为
| 3 |
| 20 |
(Ⅱ)设“密码被破译”为事件C,“密码未被破译”为事件D.
D=
| . |
| A1 |
| . |
| A2 |
| . |
| A3 |
| . |
| A1 |
| . |
| A2 |
| . |
| A3 |
P(D)=P(
| . |
| A1 |
| . |
| A2 |
| . |
| A3 |
| 4 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 2 |
| 5 |
而P(C)=1-P(D)=
| 3 |
| 5 |
故P(C)>P(D).
答:密码被破译的概率比密码未被破译的概率大.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 ,乙出现的点数为
,乙出现的点数为 ,若令
,若令 为
为 的概率,
的概率, 为
为 的概率,试求
的概率,试求 的值.
的值. .
. 的分布列和期望.
的分布列和期望.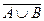 )=_________,P(AB)=___________.
)=_________,P(AB)=___________.