题目内容
甲、乙两名射击运动员,甲射击一次命中10环的概率为0.5,乙射击一次命中10环的概率为s,若他们独立的射击两次,设乙命中10环的次数为X,则EX= ,Y为甲与乙命中10环次数的差的绝对值.
,Y为甲与乙命中10环次数的差的绝对值.
求(1) s的值 (2) Y的分布列及期望.
 ,Y为甲与乙命中10环次数的差的绝对值.
,Y为甲与乙命中10环次数的差的绝对值. 求(1) s的值 (2) Y的分布列及期望.
(1)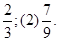
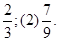
本试题主要考查了该路段求解以及分不累和期望值的求解。
解:由已知可得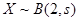 ,故
,故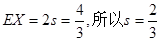 .
.
有Y的取值可以是0,1,2.
甲、乙两人命中10环的次数都是0次的概率是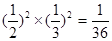 ,
,
甲、乙两人命中10环的次数都是1次的概率是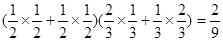 ,
,
甲、乙两人命中10环的次数都是2次的概率是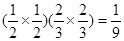 所以
所以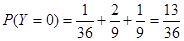 ;
;
甲命中10环的次数是2且乙命中10环的次数是0次的概率是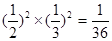 ,甲命中10环的次数是0且乙命中10环的次数是2次的概率是
,甲命中10环的次数是0且乙命中10环的次数是2次的概率是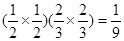
所以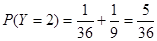 ,故
,故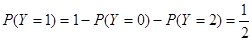 所以Y的分布列是
所以Y的分布列是
所以 Y的期望是EY=7/9.
解:由已知可得
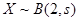 ,故
,故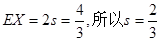 .
.有Y的取值可以是0,1,2.
甲、乙两人命中10环的次数都是0次的概率是
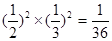 ,
,甲、乙两人命中10环的次数都是1次的概率是
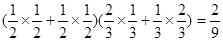 ,
,甲、乙两人命中10环的次数都是2次的概率是
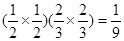 所以
所以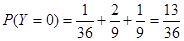 ;
; 甲命中10环的次数是2且乙命中10环的次数是0次的概率是
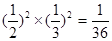 ,甲命中10环的次数是0且乙命中10环的次数是2次的概率是
,甲命中10环的次数是0且乙命中10环的次数是2次的概率是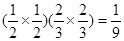
所以
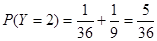 ,故
,故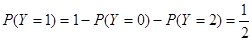 所以Y的分布列是
所以Y的分布列是| Y | 0 | 1 | 2 |
| P | 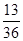 | 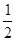 | 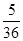 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
. 的概率;
的概率; 个点,连续取
个点,连续取 次,得到
次,得到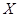 ,求
,求 的分布列和数学期望.
的分布列和数学期望. 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
. 的值;
的值; 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量 .
. 的分布表如表所示,则
的分布表如表所示,则 ▲ .
▲ .
 .
.  的概率;
的概率;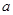 ,得2分的概率为
,得2分的概率为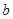 ,不得分的概率为
,不得分的概率为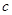 ,
,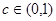 ,且无其它得分情况。已知他投篮一次得分的数学期望为1,则
,且无其它得分情况。已知他投篮一次得分的数学期望为1,则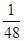
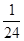
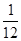
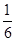
 ,则随机变量
,则随机变量 点数大于
点数大于 4时,质点向前跳两步.
4时,质点向前跳两步. 质点到达的正整数记为
质点到达的正整数记为 ,求E
,求E