题目内容
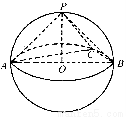
如图,多面体ABC-A1B1C1中,三角形ABC是边长为4的正三角形,AA1∥BB1∥CC1,AA1⊥平面ABC,AA1=BB1=2CC1=4.
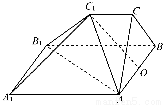
(1)若O是AB的中点,求证:OC1⊥A1B1;
(2)在线段AB1上是否存在一点D,使得CD∥平面A1B1C1,若存在,确定点D的位置;若不存在,请说明理由.
(1)见解析(2)点D是AB1的中点
【解析】(1)证明:取线段A1B1的中点E,连接OE,C1E,CO,

已知等边三角形ABC的边长为4,AA1=BB1=2CC1=4,AA1⊥平面ABC,AA1∥BB1∥CC1,
∴四边形AA1B1B是正方形,OE⊥AB,CO⊥AB,
又∵CO∩OE=O,
∴AB⊥平面EOCC1,
又A1B1∥AB,OC1?平面EOCC1,故OC1⊥A1B1,
(2)设OE∩AB1=D,则点D是AB1的中点,
∴ED∥AA1,ED=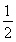 AA1,
AA1,
又∵CC1∥AA1,CC1=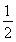 AA1,
AA1,
∴四边形CC1ED是平行四边形,∴CD∥C1E.
∵CD?平面A1B1C1,C1E?平面A1B1C1,∴CD∥平面A1B1C1,
即存在点D使得CD∥平面A1B1C1,点D是AB1的中点.

下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程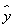 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程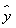 =
=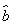 x+
x+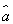 必过(
必过(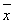 ,
,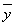 );
);
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握确认这两个变量间有关系.
其中错误的个数是( )
本题可以参考独立性检验临界值表:
P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.0 B.1 C.2 D.3