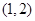题目内容
设偶函数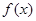 满足
满足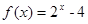 (
(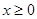 ),则
),则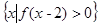 =
=
A.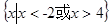 | B.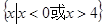 |
C. | D. |
B
解析试题分析:由偶函数满f(x)足f(x)=2x-4(x≥0),可得f(x)=f(|x|)=2|x|-4,根据偶函数的性质将函数转化为绝对值函数,再求解不等式,即由偶函数满足f(x)=2x-4(x≥0),可得f(x)=f(|x|)=2|x|-4,则f(x-2)=f(|x-2|)=2|x-2|-4,要使f(|x-2|)>0,只需2|x-2|-4>0,|x-2|>2
解得x>4,或x<0.应选B.
考点:本题主要考查偶函数性质、不等式的解法以及相应的运算能力。
点评:解答本题的关键是利用偶函数的性质将函数转化为绝对值函数,从而简化计算.

练习册系列答案
相关题目
不等式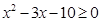 的解集是
的解集是
A.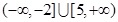 | B.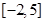 | C.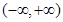 | D.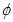 |
不等式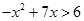 的解集是
的解集是
A.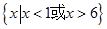 | B.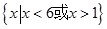 |
C.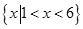 | D.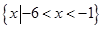 |
已知函数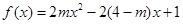 ,
,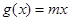 ,若对于任一实数
,若对于任一实数 ,
, 与
与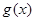 的值至少有一个为正数,则实数
的值至少有一个为正数,则实数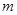 的取值范围是( )
的取值范围是( )
| A.(0,2) | B.(0,8) | C.(2,8) | D.(-∞,0) |
设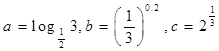 ,则( )
,则( )
A.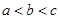 | B.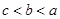 | C.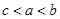 | D.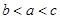 |
当a<0时,不等式42x2+ax-a2<0的解集为( )
A.{x| <x<- <x<-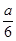 } } | B.{x|-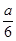 <x< <x< } } |
C.{x| <x<- <x<-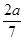 } } | D.空集 |
不等式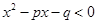 的解集是
的解集是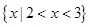 ,则不等式
,则不等式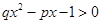 的解集是
的解集是
A.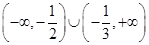 | B.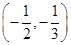 |
C.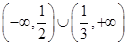 | D.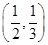 |
不等式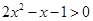 的解集是 ( )
的解集是 ( )
A.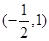 | B.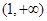 |
C.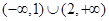 | D.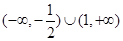 |
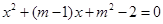 的两个实根一个小于0,另一个大于1,那么实数m的取值范围是( )
的两个实根一个小于0,另一个大于1,那么实数m的取值范围是( )