题目内容
如果方程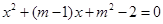 的两个实根一个小于0,另一个大于1,那么实数m的取值范围是( )
的两个实根一个小于0,另一个大于1,那么实数m的取值范围是( )
A. | B. | C. | D.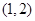 |
B
解析试题分析:方程x2+(m-1)x+m2-2=0对应的二次函数,f(x)=x2+(m-1)x+m2-2开口向上,方程x2+(m-1)x+m2-2=0的两个实根一个小于0,另一个大于1,只需f(1)<0,且f(0)<0,即为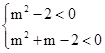 ,解二次不等式得到实数
,解二次不等式得到实数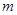 的取值范围是
的取值范围是 ,选B.
,选B.
考点:本试题主要考查了一元二次方程根的分布与系数的关系,是基础题
点评:解决该试题的关键是能结合图形得到方程对应的二次函数开口向上,方程x2+(m-1)x+m2-2=0的两个实根一个小于0,另一个大于1,只需f(1)<0,且f(0)<0可求得m的范围.

练习册系列答案
相关题目
不等式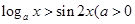 且
且 对任意
对任意 都成立,则
都成立,则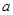 的取值
的取值
范围为
A.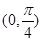 | B. | C.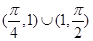 | D.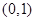 |
若不等式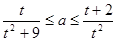 在
在 上恒成立,则
上恒成立,则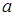 的取值范围是( )
的取值范围是( )
A.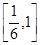 | B.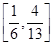 | C.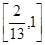 | D.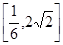 |
若不等式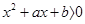 的解集为
的解集为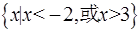 ,则
,则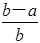 的值为( )
的值为( )
A.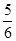 | B.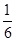 | C.—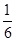 | D.— 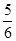 |
设偶函数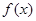 满足
满足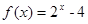 (
(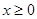 ),则
),则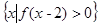 =
=
A.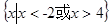 | B.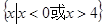 |
C. | D.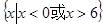 |
不等式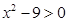 的解集为( )
的解集为( )
A.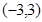 | B.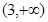 | C.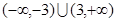 | D.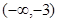 |
已知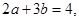 则
则 的最小值为( )
的最小值为( )
A.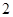 | B.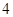 | C. | D. |
不等式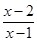 ≥0的解集是( )
≥0的解集是( )
| A.[2, +∞) | B.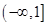 ∪(2, +∞) ∪(2, +∞) |
| C.(-∞,1) | D.(-∞,1)∪[2,+∞) |
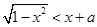 在区间
在区间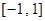 上恒成立,则实数
上恒成立,则实数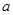 的取值范围是 .
的取值范围是 .