题目内容
椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)如果点A在圆x2+y2=c2(c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;
(2)若函数y=
| 2 |
| F2B |
| F2A |
分析:(1)根据题意判断出∴△AF1F2为一直角三角形,利用勾股定理求得|F2A|利用椭圆的定义求得|AF1|+|AF2|=2a,进而求得a和c的关系,则椭圆的离心率可得.
(2)利用函数的图象恒过定点,求得a和b,则c可求得,求得椭圆的两焦点,先看AB⊥x轴时,求得A,B的坐标,进而求得
和
的坐标,则
•
可求得;再看AB与x轴不垂直,设直线AB的方程,与椭圆的方程联立消去y,利用判别式求得k的范围,设出A,B的坐标,进而表示出x1+x2和x1x2,
和
的坐标进而求得
•
的表达式,利用k的范围确定
•
的范围.
(2)利用函数的图象恒过定点,求得a和b,则c可求得,求得椭圆的两焦点,先看AB⊥x轴时,求得A,B的坐标,进而求得
| F2A |
| F2B |
| F2A |
| F2B |
| F2A |
| F2B |
| F2A |
| F2B |
| F2A |
| F2B |
解答:解:(1)∵点A在圆x2+y2=c2上,
∴△AF1F2为一直角三角形,
∵|F1A|=c,|F1F2|=2c,∴|F2A|=
=
c
由椭圆的定义知:|AF1|+|AF2|=2a,∴c+
c=2a
∴e=
=
=
-1
(2)∵函数y=
+logmx的图象恒过点(1,
)
∴a=
,b=1,c=1,
点F1(-1,0),F2(1,0),
①若AB⊥x轴,则A(-1,
),B(-1,-
),
∴
=(-2,
),
=(-2,-
),
•
=4-
=
②若AB与x轴不垂直,设直线AB的斜率为k,则AB的方程为y=k(x+1)
由
消去y得(1+2k2)x2+4k2x+2(k2-1)=0(*)
∵△=8k2+8>0,∴方程(*)有两个不同的实根.
设点A(x1,y1),B(x2,y2),
则x1,x2是方程(*)的两个根x1+x2=-
,x1x2=
=(x1-1,y1),
=(x2-1,y2),
•
=(x1-1)(x2-1)+y1y2=(1+k2)x1x2+(k2-1)(x1+x2)+1+k2
=(1+k2)
+(k2-1)(-
)+1+k2=
=
-
∵1+2k2≥1,∴0<
≤1,0<
≤
-1≤
•
=
-
<
,
由①②知-1≤
•
<
.
∴△AF1F2为一直角三角形,
∵|F1A|=c,|F1F2|=2c,∴|F2A|=
| |F1F2|2-|AF1|2 |
| 3 |
由椭圆的定义知:|AF1|+|AF2|=2a,∴c+
| 3 |
∴e=
| c |
| a |
| 2 | ||
1+
|
| 3 |
(2)∵函数y=
| 2 |
| 2 |
∴a=
| 2 |
点F1(-1,0),F2(1,0),
①若AB⊥x轴,则A(-1,
| ||
| 2 |
| ||
| 2 |
∴
| F2A |
| ||
| 2 |
| F2B |
| ||
| 2 |
| F2A |
| F2B |
| 1 |
| 2 |
| 7 |
| 2 |
②若AB与x轴不垂直,设直线AB的斜率为k,则AB的方程为y=k(x+1)
由
|
∵△=8k2+8>0,∴方程(*)有两个不同的实根.
设点A(x1,y1),B(x2,y2),
则x1,x2是方程(*)的两个根x1+x2=-
| 4k2 |
| 1+2k2 |
| 2(k2-1) |
| 1+2k2 |
| F2A |
| F2B |
| F2A |
| F2B |
=(1+k2)
| 2(k2-1) |
| 1+2k2 |
| 4k2 |
| 1+2k2 |
| 7k2-1 |
| 1+2k2 |
| 7 |
| 2 |
| 9 |
| 2(1+2k2) |
∵1+2k2≥1,∴0<
| 1 |
| 1+2k2 |
| 9 |
| 2(1+2k2) |
| 9 |
| 2 |
-1≤
| F2A |
| F2B |
| 7 |
| 2 |
| 9 |
| 2(1+2k2) |
| 7 |
| 2 |
由①②知-1≤
| F2A |
| F2B |
| 7 |
| 2 |
点评:本题主要考查了直线与圆锥曲线的综合问题.涉及了椭圆的基本性质,向量的运算,考查了知识的综合运用和基本的运算能力.

练习册系列答案
相关题目
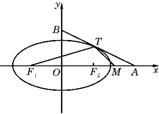 如图,椭圆
如图,椭圆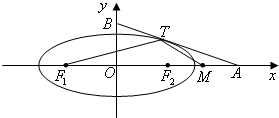 如图,椭圆
如图,椭圆