题目内容
(1)如下图所示,在正方体ABCD-A1B1C1D1中,M∈AD1,N∈BD,且D1M=DN,求证:MN∥平面CC1D1D

(2)在本题中,若M、N分别是AD1、BD的中点,求证:MN∥平面CC1D1D
答案:
解析:
提示:
解析:
(1)证法一:连结AN并延长,交直线CD于E,连结D1E.
∵AB∥CD,∴![]() .
.
∵BD=AD1,且D1M=DN,∴![]() .
.
在△AD1E中,MN∥D1E.
又MN![]() 平面CC1D1D,D1E
平面CC1D1D,D1E![]() 平面CC1D1D,
平面CC1D1D,
∴MN∥平面CC1D1D.
证法二:过点M作MP∥AD,交DD1于P,过点N作NQ∥AD交CD于点Q,连结PQ,
则MP∥NQ,在△D1AD中,![]() .
.
∵NQ∥AD,AD∥BC,∴NQ∥BC.
在△DBC中,![]() .
.
∵D1M=DN,D1A=DB,AD=BC,∴NQ=MP.
∴四边形MNQP为平行四边形,则MN∥PQ.
而MN![]() 平面CC1D1D,PQ
平面CC1D1D,PQ![]() 平面CC1D1D,
平面CC1D1D,
∴MN∥平面CC1D1D
(2)证明:∵N是BD的中点,∴N也是AC的中点.
又∵M是AD1的中点,
∴MN是△ACD1的中位线.
∴MN∥D1C.
又∵MN![]() 平面CC1D1D,D1C
平面CC1D1D,D1C![]() 平面CC1D1D,
平面CC1D1D,
∴MN∥平面CC1D1D
思路分析:(1)本题考查直线与平面平行的判定方法.要证明MN∥平面CC1D1D,根据直线和平面平行的判定定理,只需要在平面CC1D1D内找一条与MN平行的直线即可,而此直线的作法多种多样,下面给出两种证明方法.
提示:
从本题中我们可以看出,证线面平行的根本问题是要在平面内找一条直线与已知直线平行,此时常用中位线定理、成比例线段、平行移动、补形等方法,具体用何种方法要视条件而定.

练习册系列答案
相关题目



 中,
中,
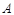 为
为 边上一点,
边上一点, 将
将 沿
沿 折起,使平面
折起,使平面 ⊥平面
⊥平面 .
. ⊥平面
⊥平面 (2)若
(2)若 是侧棱
是侧棱 把几何体分成的两部分的体积之比。
把几何体分成的两部分的体积之比。