题目内容
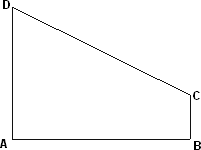
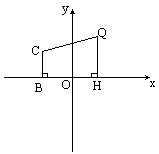
如图直角梯形CBHQ,CB=2,BH=4,HQ=3,BH的中点为原点O,一曲线过Q点且曲线上任意一点到B、H的距离之和都相等.
(1)求曲线方程;
(2)设曲线上任意一点P,求∠BPH的范围;(3)曲线上的弦以C为中点的有几条?并证明你的结论.
答案:
解析:
解析:
|
解(1)由题意曲线为椭圆,且过Q点
∵BH=4 O为中点 ∴c=2 又∵QB+QH=8 ∴a=4 解(2)设曲线上任意一点P 则|PB|+|PH|=8 又cosθ= ∵cosθ在[0,π]上单调递减 ∴θ∈[0, 解(3)有一条 证明:设过C(-2,2)的直线斜率为k. 当k=0和k不存在时,C不是弦的中点, 再设过C的直线方程为y=k(x+2)+2 代入椭圆方程 得(3+4k2)x2+16k(1+k)x+16(1+k)2-12×4=0 ∵3+4k2≠0 ∴ 有唯一解. ∴仅有一条弦 (法二反证法) |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
| |||||||||||
| |||||||||||
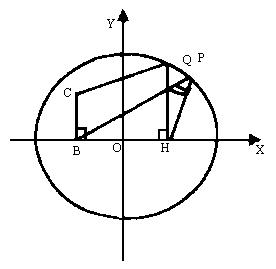
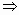 b2=12 所求方程为
b2=12 所求方程为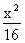 +
+ =1
=1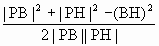 =
= =
= -1≥
-1≥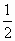
 ]
] +
+ =1
=1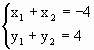
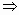 k=
k=