题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
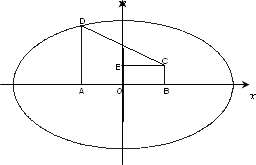
解:如图,以
则 设椭圆方程为 则 解得 ∴所求椭圆方程为 |
(2) |
解:由 显然直线 直线 不妨设直线 由 由 设 则 ∵ ∴ ∴ 解得: 由 故直线 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
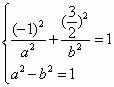
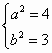 ………………4分
………………4分 得
得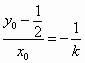 即
即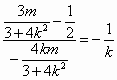
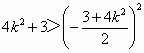 得
得 本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分.
本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分. ,
, ).
). |;若不存在,请说明理由.
|;若不存在,请说明理由.
 本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分.
本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分. ,点E,F分别为线段AB,CD的中点,则EF=________.
,点E,F分别为线段AB,CD的中点,则EF=________.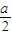 ,点E,F分别为线段AB,CD的中点,则EF= .
,点E,F分别为线段AB,CD的中点,则EF= .