题目内容
已知函数 ,其中a,b为常数.
,其中a,b为常数.(1)当a=6,b=3时,求函数f(x)的单调递增区间;
(2)若任取a∈[0,4],b∈[0,3],求函数f(x)在R上是增函数的概率.
【答案】分析:(1)将a=6,b=3代入,我们易求出函数的解析式,求出函数的导函数后,令导函数的函数值大于等于0,由此构造关于x的不等式,解不等式即可得到函数f(x)的单调递增区间;
(2)这是一个几何概型问题,我们可以先画出a∈[0,4],b∈[0,3],对应的平面区域的面积,然后再求出满足条件函数f(x)在R上是增函数时对应的平面区域的面积,计算出对应的面积后,代入几何概型公式即可得到答案.
解答: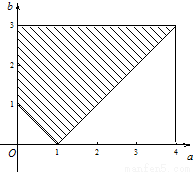 解:(1)当a=6,b=3时,
解:(1)当a=6,b=3时,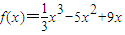 ,f'(x)=x2-10x+9
,f'(x)=x2-10x+9
令f'(x)=x2-10x+9≥0,(x-1)(x-9)≥0,解得x≤1或x≥9,
故函数f(x)的单调递增区间分别为(-∞,1]和[9,+∞)
(2)f'(x)=x2-2(a-1)x+b2
若函数f(x)在R上是增函数,则对于任意x∈R,f'(x)≥0恒成立.
所以,△=4(a-1)2-4b2≤0,即(a+b-1)(a-b-1)≤0
设“f(x)在R上是增函数”为事件A,则事件A对应的区域为(a,b)|(a+b-1)(a-b-1)≤0
全部试验结果构成的区域Ω=(a,b)|0≤a≤4,0≤b≤3,如图.
所以,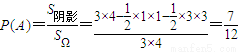
故函数f(x)在R上是增函数的概率为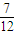 .
.
点评:本题考查的知识点是利用导数研究函数的单调性,几何概型及概率的应用,其中利用导函数大于等于0,则函数在该区间上单调递增,是解答本题的关键.
(2)这是一个几何概型问题,我们可以先画出a∈[0,4],b∈[0,3],对应的平面区域的面积,然后再求出满足条件函数f(x)在R上是增函数时对应的平面区域的面积,计算出对应的面积后,代入几何概型公式即可得到答案.
解答:
 解:(1)当a=6,b=3时,
解:(1)当a=6,b=3时,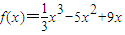 ,f'(x)=x2-10x+9
,f'(x)=x2-10x+9令f'(x)=x2-10x+9≥0,(x-1)(x-9)≥0,解得x≤1或x≥9,
故函数f(x)的单调递增区间分别为(-∞,1]和[9,+∞)
(2)f'(x)=x2-2(a-1)x+b2
若函数f(x)在R上是增函数,则对于任意x∈R,f'(x)≥0恒成立.
所以,△=4(a-1)2-4b2≤0,即(a+b-1)(a-b-1)≤0
设“f(x)在R上是增函数”为事件A,则事件A对应的区域为(a,b)|(a+b-1)(a-b-1)≤0
全部试验结果构成的区域Ω=(a,b)|0≤a≤4,0≤b≤3,如图.
所以,
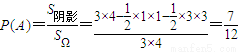
故函数f(x)在R上是增函数的概率为
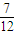 .
.点评:本题考查的知识点是利用导数研究函数的单调性,几何概型及概率的应用,其中利用导函数大于等于0,则函数在该区间上单调递增,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,其中a,b∈R.
,其中a,b∈R. ,不等式f(x)≤10在
,不等式f(x)≤10在 上恒成立,求b的取值范围.
上恒成立,求b的取值范围. ,其中a,b∈R.
,其中a,b∈R. ,不等式f(x)≤10在
,不等式f(x)≤10在 上恒成立,求b的取值范围.
上恒成立,求b的取值范围. (其中a,b为常数且
(其中a,b为常数且 )的反函数的图象经过点A(4,1)和B(16,3)。
)的反函数的图象经过点A(4,1)和B(16,3)。 在
在 上恒成立,求实数m的取值范围。
上恒成立,求实数m的取值范围。